Lecture
In Chapter 16, we familiarized ourselves with the general rules for linear transformations of random functions, presented in the form of canonical expansions. These rules are reduced to the fact that with linear transformations of random functions, their expectation and coordinate functions undergo the same linear transformations. Thus, the problem of linear transformation of a random function is reduced to the problem of the same linear transformation of several non-random functions.
In the case of linear transformations of stationary random functions, the problem can be simplified even more.
If and input impact 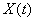 and system response
and system response  are stationary, the task of transforming a random function can be reduced to the transformation of a single non-random function — the spectral density
are stationary, the task of transforming a random function can be reduced to the transformation of a single non-random function — the spectral density 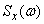 .
.
In order for stationary effects to react, the system could also be stationary, it is obviously necessary that the parameters of the system (for example, the resistances, capacitances, inductances, etc.) included in it are constant, not variable. We agree to call a linear system with constant parameters a stationary linear system. Usually the operation of a stationary linear system is described by linear differential equations with constant coefficients.
We consider the problem of transforming a stationary random function by a stationary linear system. Let the input of the linear system  stationary random function arrives
stationary random function arrives 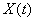 ; system response is a random function
; system response is a random function  rice (17.5.1).
rice (17.5.1).
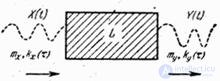
Fig. 17.5.1.
The characteristics of the random function are known. 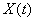 : expected value
: expected value 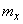 and correlation function
and correlation function 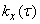 . Required to determine the characteristics of a random function
. Required to determine the characteristics of a random function  at the output of the linear system.
at the output of the linear system.
Since to solve the problem we have to transform non-random functions — expectation and coordinate functions, we will first consider the problem of determining the response of the system  on non-random exposure
on non-random exposure 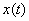 .
.
We write in operator form a linear differential equation with constant coefficients, connecting the reaction of the system 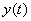 with impact
with impact 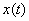 :
:
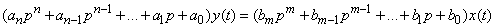 . (17.5.1)
. (17.5.1)
Where 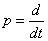 - differentiation operator.
- differentiation operator.
Equation (17.5.1) can be shorter written as:
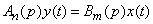 , (17.5.2)
, (17.5.2)
or, finally, conditionally solving equation (17.5.2) with respect to 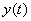 , write the system operator in "explicit" form:
, write the system operator in "explicit" form:
 . (17.5.3)
. (17.5.3)
System reaction  on impact
on impact 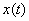 can be found by solving a linear differential equation (17.5.1). As is known from the theory of differential equations, this solution consists of two terms:
can be found by solving a linear differential equation (17.5.1). As is known from the theory of differential equations, this solution consists of two terms: 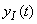 and
and 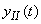 . Term
. Term 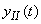 is a solution to an equation without the right side and determines the so-called free or natural oscillations of the system These are oscillations made by the system in the absence of an input, if the system at the initial moment was somehow brought out of equilibrium. In practice, the so-called sustainable systems are the most common; in these systems, free oscillations fade out with time.
is a solution to an equation without the right side and determines the so-called free or natural oscillations of the system These are oscillations made by the system in the absence of an input, if the system at the initial moment was somehow brought out of equilibrium. In practice, the so-called sustainable systems are the most common; in these systems, free oscillations fade out with time.
If we confine ourselves to considering the time intervals sufficiently distant from the beginning of the process, when all transients in the system can be considered complete, and the system operates in steady state, the second term can be discarded. 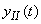 and confine ourselves to considering only the first term
and confine ourselves to considering only the first term 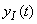 . This first term defines the so-called forced oscillations of the system under the influence of a given function on it.
. This first term defines the so-called forced oscillations of the system under the influence of a given function on it. 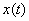 .
.
In the case where the impact 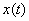 is a fairly simple analytical function, it is often possible to find the reaction of the system also in the form of a simple analytical function. In particular, when the impact is a harmonic oscillation of a certain frequency, the system responds to it also with a harmonic oscillation of the same frequency, but changed in amplitude and phase.
is a fairly simple analytical function, it is often possible to find the reaction of the system also in the form of a simple analytical function. In particular, when the impact is a harmonic oscillation of a certain frequency, the system responds to it also with a harmonic oscillation of the same frequency, but changed in amplitude and phase.
Since the coordinate functions of the spectral decomposition of a stationary random function 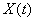 represent harmonic oscillations, we first need to learn how to determine the response of the system to the harmonic oscillation of a given frequency
represent harmonic oscillations, we first need to learn how to determine the response of the system to the harmonic oscillation of a given frequency 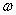 . This problem is solved very simply, especially if the harmonic oscillation is presented in a complex form.
. This problem is solved very simply, especially if the harmonic oscillation is presented in a complex form.
Let the harmonic oscillation of the form enter the system input:
 . (17.5.4)
. (17.5.4)
We will look for the reaction of the system 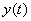 also in the form of harmonic frequency oscillations
also in the form of harmonic frequency oscillations 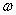 but multiplied by some complex multiplier
but multiplied by some complex multiplier 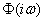 :
:
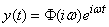 . (17.5.5)
. (17.5.5)
Factor 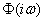 we will find as follows. We substitute the function (17.5.4) into the right, and the function (17.5.5) into the left side of equation (17.5.1). We get:
we will find as follows. We substitute the function (17.5.4) into the right, and the function (17.5.5) into the left side of equation (17.5.1). We get:
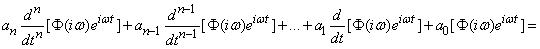
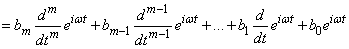 . (17.5.6)
. (17.5.6)
Meaning that with any 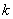
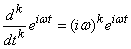 ,
, 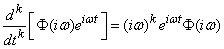 ,
,
and dividing both sides of equation (17.5.6) by 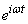 , we get:
, we get:
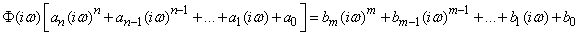 . (17.5.7)
. (17.5.7)
We see that the multiplier at 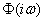 is nothing but a polynomial
is nothing but a polynomial  in which instead of the differentiation operator
in which instead of the differentiation operator 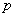 substituted
substituted 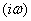 ; likewise, the right-hand side of (17.5.7) is nothing but
; likewise, the right-hand side of (17.5.7) is nothing but 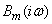 . Equation (17.5.7) can be written as:
. Equation (17.5.7) can be written as:
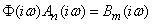 ,
,
from where
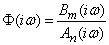 . (17.5.8)
. (17.5.8)
Function 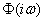 carries a special name for the frequency response of a linear system. To determine the frequency response, it is sufficient to explicitly write the system operator (17.5.3) instead of the differentiation operator
carries a special name for the frequency response of a linear system. To determine the frequency response, it is sufficient to explicitly write the system operator (17.5.3) instead of the differentiation operator 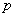 to substitute
to substitute 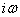 .
.
Thus, if the input of a linear system with constant parameters receives a harmonic oscillation of the form 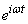 the system response is represented as the same harmonic oscillation multiplied by the frequency response of the system
the system response is represented as the same harmonic oscillation multiplied by the frequency response of the system 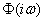 . Let the input of the system receive the effect of the form
. Let the input of the system receive the effect of the form
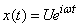 , (17.5.9)
, (17.5.9)
Where 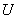 - some value independent of
- some value independent of 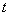 . By virtue of the linearity of the system
. By virtue of the linearity of the system 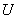 beyond the operator’s sign, and the system’s response to the impact (17.5.9) will be equal to:
beyond the operator’s sign, and the system’s response to the impact (17.5.9) will be equal to:
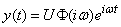 . (5/17/10)
. (5/17/10)
Obviously, this property will remain in the case when the value 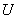 will be random (as long as it does not depend on
will be random (as long as it does not depend on 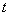 ).
).
We apply the above techniques for converting harmonic oscillations by a linear system to the expectation of a random function. 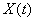 and coordinate functions of its spectral decomposition.
and coordinate functions of its spectral decomposition.
Imagine expectation 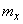 stationary random function
stationary random function 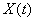 as harmonic oscillation zero frequency
as harmonic oscillation zero frequency 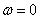 and put in the formula (17.5.8)
and put in the formula (17.5.8) 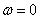 :
:
 , (17.5.11)
, (17.5.11)
where we get the expectation at the system output:
 . (5/17/12)
. (5/17/12)
Let us turn to the transformation by the linear system of the essentially random part of the function 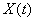 namely functions
namely functions
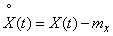 . (5/17/13)
. (5/17/13)
For this we present the function 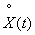 Location on
Location on  in the form of spectral decomposition:
in the form of spectral decomposition:
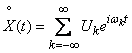 , (17.5.14)
, (17.5.14)
Where 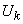 - uncorrelated random variables whose dispersions form the spectrum of a random function
- uncorrelated random variables whose dispersions form the spectrum of a random function 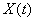 .
.
Consider a separate component of this sum:
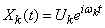 . (05/17/15)
. (05/17/15)
The response of the system to this effect will be:
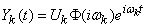 . (05/17/16)
. (05/17/16)
According to the principle of superposition, the response of the system to the sum of the impact is equal to the sum of the reactions to the individual impacts. Therefore, the response of the system to the impact (17.5.14) can be represented as a spectral decomposition:
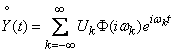 ,
,
or denoting 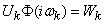 ,
,
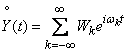 , (17.5.17)
, (17.5.17)
Where 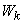 - uncorrelated random variables with mathematical expectations equal to zero.
- uncorrelated random variables with mathematical expectations equal to zero.
Let us determine the spectrum of this decomposition. For this we find the variance of the complex random variable 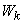 in the decomposition (17.5.17). Bearing in mind that the variance of a complex random variable is equal to the mathematical expectation of the square of its module, we have:
in the decomposition (17.5.17). Bearing in mind that the variance of a complex random variable is equal to the mathematical expectation of the square of its module, we have:
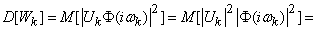
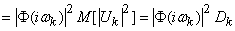 . (17.5.18)
. (17.5.18)
We come to the following conclusion: when a stationary random function is transformed by a stationary linear system, each of its ordinates is multiplied by the square of the module of the frequency response of the system for the corresponding frequency.
Thus, when a stationary random function passes through a linear stationary system, its spectrum is rearranged in a certain way: some frequencies are amplified, some, on the contrary, are weakened (filtered). The square of the frequency response module (depending on 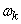 ) and shows how the system responds to oscillations of a particular frequency.
) and shows how the system responds to oscillations of a particular frequency.
In the same way as it was done before, in the spectral representation of a random function we proceed to the limit as  and from the discrete spectrum to spectral density. Obviously, the spectral density at the output of a linear system is obtained from the spectral density at the input by the same multiplication by
and from the discrete spectrum to spectral density. Obviously, the spectral density at the output of a linear system is obtained from the spectral density at the input by the same multiplication by 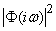 as the ordinates of the discrete spectrum:
as the ordinates of the discrete spectrum:
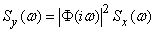 . (05/17/19)
. (05/17/19)
Thus, a very simple rule is obtained:
When a stationary random function is transformed by a stationary linear system, its spectral density is multiplied by the square of the modulus of the frequency response of the system.
Using this rule, we can easily solve the above problem: according to the characteristics of a random function at the input of a linear system, find the characteristics of a random function at its output.
Suppose that a stationary random function arrives at the input of a stationary linear system with operator (17.5.3) 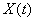 with mathematical expectation
with mathematical expectation 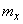 and correlation function
and correlation function 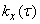 .It is required to find the mathematical expectation
.It is required to find the mathematical expectation 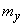 and the correlation function of a
and the correlation function of a 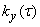 random function
random function  at the output of the system.
at the output of the system.
We will solve the problem in the following order.
1. Find the expectation of the output:
 . (05/17/20)
. (05/17/20)
2. Using the correlation function, 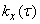 we find the spectral density at the input (see formula (17.4.12)):
we find the spectral density at the input (see formula (17.4.12)):
 . (17.5.21)
. (17.5.21)
3. According to the formula (17.5.8) we find the frequency response of the system and the square of its module:
 . (17.5.22)
. (17.5.22)
4. Multiplying the spectral density at the input to the square of the frequency response module, we find the spectral density at the output:
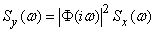 . (17.5.23)
. (17.5.23)
5. By spectral density,  we find the correlation function.
we find the correlation function.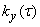 system output:
system output:
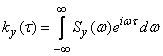 . (17.5.24)
. (17.5.24)
Thus, the problem is solved.
In many problems of practice, we are not interested in the entire correlation function 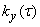 at the output of the system, but only in the variance
at the output of the system, but only in the variance  equal to
equal to
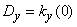 .
.
Then from formula (17.5.24) we obtain with a 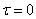 much simpler formula:
much simpler formula:
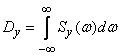 ,
,
or, given the parity of the function  ,
,
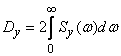 . (17.5.25)
. (17.5.25)
Example. The work of a linear dynamic system is described by a linear differential equation of the first order:
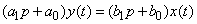 , (17.5.26)
, (17.5.26)
or
 .
.
The stationary random function is input to the system. 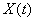 with mathematical expectation
with mathematical expectation 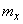 and correlation function
and correlation function
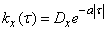 , (17.5.27)
, (17.5.27)
Where  - positive coefficient (see example 1
- positive coefficient (see example 1  17.4). Find expectation
17.4). Find expectation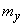 and variance
and variance  at the output of the system.
at the output of the system.
Decision. According to the formula (17.5.20) we have:
 .
.
Obviously the magnitude 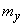 does not depend on the parameter
does not depend on the parameter  , increases with increasing
, increases with increasing  and decreases with increasing
and decreases with increasing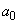 .
.
Спектральную плотность на входе определяем как в примере 1 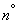 17.4:
17.4:
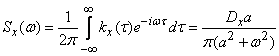
(см. рис. 17.4.4).
По формуле (17.5.8) находим частотную характеристику системы:
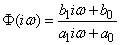
и квадрат ее модуля:
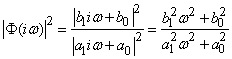 .
.
Затем определяем спектральную плотность на выходе системы:
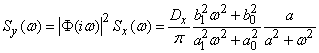 .
.
Далее по формуле (17.5.25) определяем дисперсию на выходе:
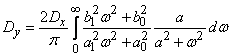 .
.
Для вычисления интеграла разложим подынтегральное выражение на простые дроби:
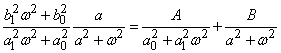
и определим коэффициенты:
 ;
;
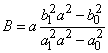 .
.
После интегрирования получим:
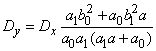 .
.
В заключение данного 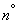 упомянем о том, как преобразуется линейной системой стационарная случайная функция, содержащая в качестве слагаемого обычную случайную величину:
упомянем о том, как преобразуется линейной системой стационарная случайная функция, содержащая в качестве слагаемого обычную случайную величину:
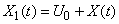 , (17.5.28)
, (17.5.28)
Where 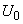 - случайная величина с дисперсией
- случайная величина с дисперсией 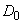 ,
, 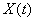 - стационарная случайная функция.
- стационарная случайная функция.
The response of the system to exposure 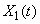 ) is found as the sum of the reactions to individual actions on the right-hand side (17.5.28). The reaction to the impact,
) is found as the sum of the reactions to individual actions on the right-hand side (17.5.28). The reaction to the impact, 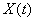 we can already find. Impact
we can already find. Impact 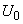 we will consider as harmonic oscillation of zero frequency
we will consider as harmonic oscillation of zero frequency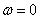 ; according to the formula (17.5.11) the reaction to it will be equal to
; according to the formula (17.5.11) the reaction to it will be equal to
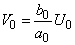 . (17.5.29)
. (17.5.29)
Term 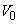 just add to the response of the system to the impact
just add to the response of the system to the impact 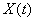 .
.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis