Lecture
The table shows the main generating functions that are usually required for solving typical problems. All sums ∑ are performed on the variable n from 0 to ∞, unless otherwise specified. Sequence elements are numbered from 0.

The generating functions proposed for consideration are a kind of “alphabet”, or, if you like, a “multiplication table” for the theory of generating functions. Understanding these generating functions will allow you to work with more complex expressions, and knowledge of the table will speed up many oral calculations.
The first and second generating functions are derived directly from the definition (see “Introduction”). The third sequence is described in detail in the appendix “On the 1 / (1 − z) expansion”.
The generating function of sequence No. 4 is obtained by replacing z with −z in the function for sequence No. 3. The generating functions for sequences No. 5, No. 7, and No. 8 are obtained in the same way: they must be replaced in the third generating function and z by z m , 2z and rz, respectively.
The generating function of the sequence # 6 is obtained by differentiating the function # 3:
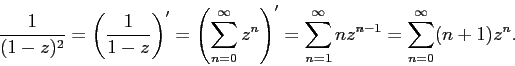
Exactly the same result is obtained if we use the binomial series (see “Extended binomial coefficients”):
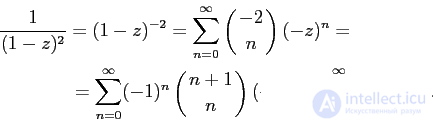
Quite similarly, you need to deal with the generating function of sequences No. 10 and No. 11:
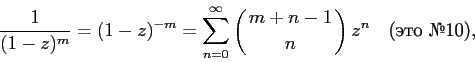
if we now replace m with m + 1 and use the fact that for whole positive ones, the identity is true 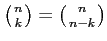 Then we get the eleventh row of the table:
Then we get the eleventh row of the table:
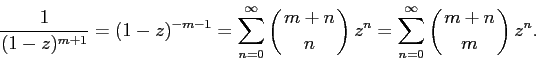
The sequence No. 9 and the generating function for it follow from the binomial theorem (after replacing a by z, and b by 1), the statement of which is proved in the course of combinatorics:
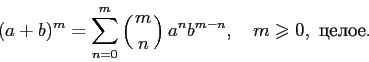
The generating function for the sequence # 12 is obtained by integrating the generating function for the sequence # 3 (we assume that the integration constant is zero, so that a 0 = 0 is satisfied):
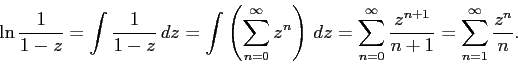
Sequence # 13 is obtained in the same way, but with an additional change of z by −z and multiplying the result by −1.
Expansion in a number of exponents (row number 14 of the table) is known from the course of mathematical analysis. By the Taylor formula, the coefficient at z n is a derivative of order n, calculated at zero divided by n !:
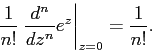
Moreover, the series for the exponent converges for any complex z (if, of course, we assume that z is a number).
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis