Lecture
In the previous chapter, we met with a very convenient mathematical apparatus of probability theory - with the apparatus of numerical characteristics. In many cases, this apparatus allows one to find the numerical characteristics of the functions of random variables (first of all, the expectation and variance) according to the numerical characteristics of the arguments, leaving the distribution laws completely out of the way. Such methods of direct determination of numerical characteristics are applicable mainly to linear functions.
In practice, very often there are cases when the studied function of random variables, although not strictly linear, differs little from linear in practice and can be approximately replaced by linear in solving problems. This is due to the fact that in many practical problems, random changes in the quantities appearing in them act as minor “errors” superimposed on the basic pattern. Due to the comparative smallness of these errors, the functions usually appearing in the problem, not being linear in the entire range of variation of their arguments, turn out to be almost linear in a narrow range of their random changes.
Indeed, it is known from mathematics that any continuous differentiable function in a fairly narrow range of variation of the arguments can be approximately replaced by a linear (linearized) function. The error that occurs in this case is, the smaller, the narrower the boundaries of the arguments change and the closer the function is to the linear one. If the area of practically possible values of random arguments is so small that in this area a function can be linearized with sufficient accuracy for practice, then replacing a nonlinear function with a linear one, you can apply to the latter that apparatus of numerical characteristics that is designed for linear functions. Knowing the numerical characteristics of the arguments, it will be possible to find the numerical characteristics of the function. Of course, at the same time we will get only an approximate solution of the problem, but in most cases the exact solution is not required.
When solving practical problems in which random factors manifest themselves in the form of insignificant perturbations imposed on the basic laws, linearization almost always turns out to be possible precisely because of the smallness of random perturbations.
Consider, for example, the problem of external ballistics on the movement of the center of mass of a projectile. Projectile range 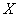 defined as some function of shooting conditions - throw angle
defined as some function of shooting conditions - throw angle 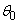 initial speed
initial speed 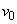 and ballistic coefficient
and ballistic coefficient 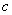 :
:
 . (11.1.1)
. (11.1.1)
The function (11.1.1) is nonlinear if we consider it over the entire range of variation of the arguments. Therefore, when it comes to solving the main problem of external ballistics, the function (11.1.1) acts as a nonlinear one and cannot be linearized. However, there are tasks in which such functions are linearized; these are tasks related to the study of errors or errors. Let us be interested in a random error in the range of the projectile 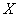 associated with the presence of a number of random factors: inaccuracy of setting the angle
associated with the presence of a number of random factors: inaccuracy of setting the angle 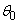 , vibrations of the barrel when fired, ballistic inhomogeneity of shells, different weights of charges, etc. Then we fix certain nominal shooting conditions and we will consider random deviations from these conditions. The range of such random changes is usually small, and the function
, vibrations of the barrel when fired, ballistic inhomogeneity of shells, different weights of charges, etc. Then we fix certain nominal shooting conditions and we will consider random deviations from these conditions. The range of such random changes is usually small, and the function 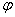 without being linear in the whole range of changes in its arguments, it can be linearized in a small area of their random changes.
without being linear in the whole range of changes in its arguments, it can be linearized in a small area of their random changes.
The method of linearization of functions depending on random arguments is widely used in various fields of engineering. Very often, having received the solution of the problem by the usual methods of the “exact sciences”, it is desirable to estimate the possible errors in this solution related to the influence of random factors not taken into account when solving the problem. In this case, as a rule, the problem of estimating the error is successfully solved by the method of linearization, since the random changes in the quantities involved in the problem are usually small. If this were not the case, and random changes in the arguments went beyond the region of approximate linearity of functions, the technical solution should be considered unsatisfactory, since it would contain too much of an element of uncertainty.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis