11.2. Linearize the function of one random argument

In practice, the need to linearize the function of one random argument is relatively rare: usually the cumulative effect of several random factors has to be taken into account. However, from methodological considerations it is convenient to start from this simplest case. Let there be a random variable 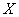and its numerical characteristics are known: expectation and variance .

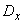Assume that practically possible values ​​of a random variable 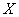limited to 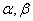i.e.

.

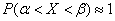There is another random variable. 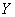related to 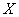functional dependence:

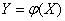, (11.2.1)

and function 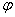although not linear, it differs little from linear in the segment .

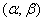Required to find the numerical characteristics of 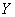- expected value 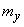and variance .

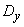Consider the curve Location on 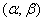(fig. 11.2.1) and replace it with an approximately tangent at the point 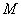with abscissa . The tangent equation is:

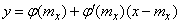. (11.2.2)

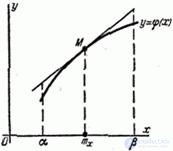
Fig. 11.2.1

Suppose that the interval of practically possible values ​​of the argument 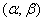so narrow that within this interval the curve and the tangent differ little, so that the curve section can practically be replaced by the tangent section; in short, on the site 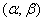function almost linear. Then random variables 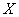and 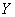approximately related linear dependence:

,

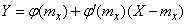or denoting ,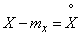

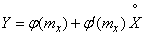. (11.2.3)

To the linear function (11.2.3), one can apply the well-known methods of determining the numerical characteristics of linear functions (see 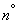10.2). The mathematical expectation of this linear function will be found by substituting in its expression (11.2.3) the mathematical expectation of the argument 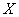equal to zero. We get:

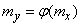. (11.2.4)

Variance of magnitude 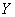determined by the formula

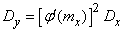. (11.2.5)

Turning to the standard deviation, we have:

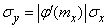. (11.2.6)

Formulas (11.2.4), (11.2.5), (11.2.6), of course, are approximate, since the replacement of a nonlinear function by a linear one is also approximate.

Thus, we solved the task and came to the following conclusions.

To find the expectation of an almost linear function, you need to substitute its expectation instead of an argument in the function expression. To find the variance of an almost linear function, the variance of the argument must be multiplied by the square of the derivative of the function at the point corresponding to the expectation of the argument.