Lecture
The consequence of both main theorems - the theorem of addition of probabilities and the theorem of multiplication of probabilities - is the so-called formula of full probability.
Let it be required to determine the probability of some event. 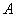 which can happen with one of the following events:
which can happen with one of the following events:
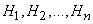 ,
,
forming a complete group of incompatible events. We will call these events hypotheses.
Let us prove that in this case
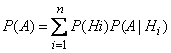 , (3.4.1)
, (3.4.1)
those. event probability 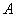 calculated as the sum of the products of the probability of each hypothesis on the probability of an event with this hypothesis.
calculated as the sum of the products of the probability of each hypothesis on the probability of an event with this hypothesis.
Formula (3.4.1) is called the formula of total probability.
Evidence. Since the hypotheses 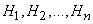 form a complete group then event
form a complete group then event 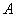 can only appear in combination with any of these hypotheses:
can only appear in combination with any of these hypotheses:
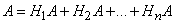 .
.
Since the hypotheses 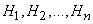 incompatible, then combinations
incompatible, then combinations 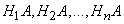 also inconsistent; applying to them the addition theorem, we get:
also inconsistent; applying to them the addition theorem, we get:
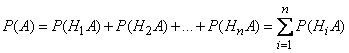 .
.
Applying to event  multiplication theorem, we get:
multiplication theorem, we get:
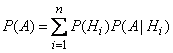 ,
,
Q.E.D.
Example 1. There are three identical-looking bins; in the first urn there are two white and one black ball; in the second - three white and one black; in the third - two white and two black balls. Someone chooses one of the urns at random and takes the ball out of it. Find the probability that this ball is white.
Decision. Consider three hypotheses:
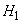 - the choice of the first urn,
- the choice of the first urn,
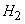 - the choice of the second urn,
- the choice of the second urn,
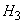 - choice of the third urn
- choice of the third urn
and event 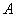 - the appearance of a white ball.
- the appearance of a white ball.
Since the hypotheses, according to the condition of the problem, are equally possible,
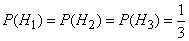 .
.
Conditional probabilities of events 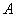 with these hypotheses are respectively equal:
with these hypotheses are respectively equal:
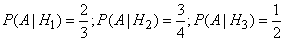 .
.
By the formula of total probability
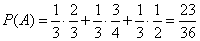 .
.
Example 2. The plane is three single shots. The probability of hitting the first shot is 0.4, at the second - 0.5, at the third 0.7. To bring the aircraft out of action, three hits are obviously enough; with one hit the plane crashes with a probability of 0.2, with two hits - with a probability of 0.6. Find the probability that as a result of three shots the plane will be disabled.
Decision. Consider four hypotheses:
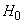 - not a single shell hit the plane,
- not a single shell hit the plane,
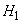 - one projectile hit the plane,
- one projectile hit the plane,
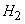 - two shells hit the plane,
- two shells hit the plane,
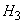 - Three projectiles hit the plane.
- Three projectiles hit the plane.
Using the theorems of addition and multiplication, we find the probabilities of these hypotheses:
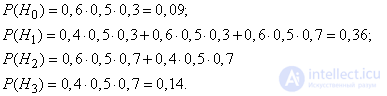
Conditional probabilities of events 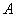 (aircraft failure) with these hypotheses are:
(aircraft failure) with these hypotheses are:
 .
.
Using the formula of total probability, we get:
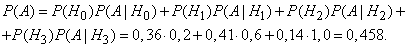
Note that the first hypothesis 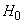 it would be possible not to introduce it into consideration, since the corresponding term in the formula of the full probability vanishes. This is usually the case when applying the formula of full probability, considering not the full group of incompatible hypotheses, but only those of which this event is possible.
it would be possible not to introduce it into consideration, since the corresponding term in the formula of the full probability vanishes. This is usually the case when applying the formula of full probability, considering not the full group of incompatible hypotheses, but only those of which this event is possible.
Example 3. The engine is controlled by two regulators. Considered a specific period of time 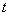 during which it is desirable to ensure trouble-free operation of the engine. In the presence of both regulators, the engine refuses with probability
during which it is desirable to ensure trouble-free operation of the engine. In the presence of both regulators, the engine refuses with probability  , when only the first of them works - with probability
, when only the first of them works - with probability  , at work only the second -
, at work only the second - 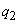 , in case of failure of both regulators - with probability
, in case of failure of both regulators - with probability  . The first regulator has reliability
. The first regulator has reliability 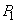 second -
second - 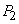 . All elements fail independently of each other. Find the full reliability (probability of failure-free operation) of the engine.
. All elements fail independently of each other. Find the full reliability (probability of failure-free operation) of the engine.
Decision. Consider the hypotheses:
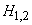 - both regulators work,
- both regulators work,
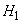 - only the first regulator is working (the second one has failed),
- only the first regulator is working (the second one has failed),
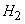 - only the second regulator works (the first one is out of order),
- only the second regulator works (the first one is out of order),
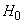 - both regulators have failed
- both regulators have failed
and event
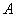 - engine uptime.
- engine uptime.
The probabilities of hypotheses are:

Conditional probabilities of events 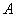 with these hypotheses are given:
with these hypotheses are given:
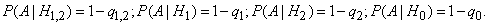
According to the formula of the total probability we get:
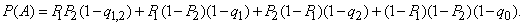
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis