Lecture
As a lemma, which is necessary for the proof of theorems belonging to the group of the “law of large numbers,” we will prove one very general inequality, known as the Chebyshev inequality.
Let there be a random variable 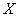 with mathematical expectation
with mathematical expectation 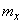 and variance
and variance 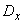 . Chebyshev's inequality states that, whatever the positive number
. Chebyshev's inequality states that, whatever the positive number  the probability that the magnitude
the probability that the magnitude 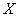 deviate from their expectation by no less than
deviate from their expectation by no less than  , bounded above by value
, bounded above by value  :
:
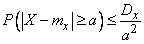 . (13.2.1)
. (13.2.1)
Evidence. 1. Let the value 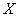 discontinuous, with a number of distribution
discontinuous, with a number of distribution
|
|
|
|
|
|
|
|
|
|
We depict the possible values of 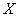 and its expectation
and its expectation 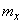 in the form of points on the number axis
in the form of points on the number axis 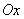 (fig. 13.2.1).
(fig. 13.2.1).

Fig. 13.2.1.
Let's set some value 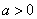 and calculate the probability that the magnitude
and calculate the probability that the magnitude 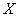 deviate from their expectation by no less than
deviate from their expectation by no less than  :
:
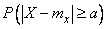 . (13.2.2)
. (13.2.2)
To do this, set aside from the point 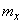 right and left along the length segment
right and left along the length segment  ; get the segment
; get the segment 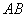 . Probability (13.2.2) is nothing but the probability that a random point
. Probability (13.2.2) is nothing but the probability that a random point 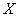 will not fall inside the segment
will not fall inside the segment 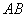 , and outside it:
, and outside it:
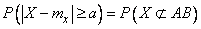 .
.
In order to find this probability, you need to sum up the probabilities of all those values 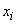 which lie outside the segment
which lie outside the segment 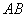 . We will write this as follows:
. We will write this as follows:
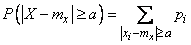 (13.2.3)
(13.2.3)
where is the record 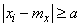 under the sum sign means that the summation applies to all those values
under the sum sign means that the summation applies to all those values  for which points
for which points 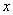 , lie outside the segment
, lie outside the segment 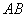 .
.
On the other hand, we write the expression for the variance of 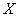 . By definition:
. By definition:
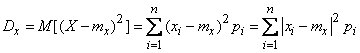 . (13.2.4)
. (13.2.4)
Since all members of the sum (13.2.4) are non-negative, it can only decrease if we do not extend it to all values 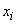 , but only on some, in particular on those that lie outside the segment
, but only on some, in particular on those that lie outside the segment  :
:
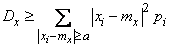 . (13.2.5)
. (13.2.5)
Replace the expression with the sum sign 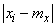 through
through  . Since for all members of the sum
. Since for all members of the sum 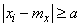 then the amount of such a replacement can also only decrease; means
then the amount of such a replacement can also only decrease; means
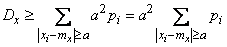 . (13.2.6)
. (13.2.6)
But according to formula (13.2.3), the sum on the right side of (13.2.6) is nothing more than the probability of a random point falling outside the segment  ; Consequently,
; Consequently,
 ,
,
whence the derived inequality directly follows.
2. In the case where the value 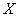 is continuous, the proof is carried out in a similar way with the replacement of probabilities
is continuous, the proof is carried out in a similar way with the replacement of probabilities 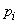 element of probability, and finite sums - integrals. Really,
element of probability, and finite sums - integrals. Really,
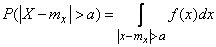 . (13.2.7)
. (13.2.7)
Where 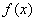 - distribution density
- distribution density 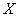 . Next, we have:
. Next, we have:

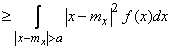 ,
,
where is the sign 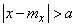 under the integral means that the integration extends to the outer part of the segment
under the integral means that the integration extends to the outer part of the segment 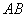 .
.
Replacing 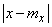 under the sign of the integral through
under the sign of the integral through  , we get:
, we get:
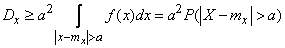 ,
,
whence Chebyshev's inequality for continuous quantities follows.
Example. Given a random variable 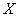 with mathematical expectation
with mathematical expectation 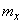 and variance
and variance 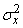 . Estimate the top probability of the magnitude
. Estimate the top probability of the magnitude 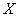 deviate from their expectation by no less than
deviate from their expectation by no less than 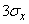 .
.
Decision. Believing in Chebyshev's inequality 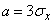 , we have:
, we have:
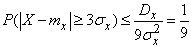 ,
,
i.e. the probability that the deviation of a random variable from its expectation will go beyond the three mean square deviations cannot be greater than 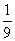 .
.
Note. Chebyshev inequality gives only the upper limit of the probability of a given deviation. Above this limit, probability cannot be under any distribution law. In practice, in most cases the probability that the magnitude 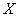 go outside the lot
go outside the lot 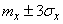 , significantly less
, significantly less 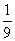 . For example, for a normal law, this probability is approximately equal to 0.003. In practice, most often we deal with random variables, the values of which only very rarely go beyond
. For example, for a normal law, this probability is approximately equal to 0.003. In practice, most often we deal with random variables, the values of which only very rarely go beyond 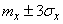 . If the distribution law of a random variable is unknown, but only
. If the distribution law of a random variable is unknown, but only 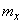 and
and 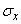 , in practice, the segment is usually considered
, in practice, the segment is usually considered 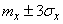 a section of practically possible values of a random variable (the so-called “three sigma rule”).
a section of practically possible values of a random variable (the so-called “three sigma rule”).
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis