6.2. Moments of normal distribution

We have proved above that the expectation of a random variable subject to the normal law (6.1.1) is equal to 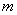and the standard deviation is .

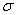We derive general formulas for central moments of any order.

By definition:

.

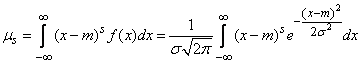Doing a variable change

,

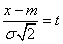we will receive:

. (6.2.1)

Applying to the expression (6.2.1) the integration formula in parts:

.

Bearing in mind that the first term inside the brackets is zero, we get:

. (6.2.2)

From the formula (6.2.1) we have the following expression for :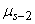

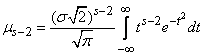. (6.2.3)

Comparing the right-hand sides of formulas (6.2.2) and (6.2.3), we see that they differ only by the factor 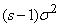; Consequently,

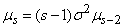. (6.2.4)

Formula (6.2.4) is a simple recurrence relation that allows expressing higher order moments in terms of lower order moments. Using this formula and bearing in mind that 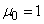and 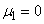, it is possible to calculate the central moments of all orders. Because 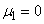, then from formula (6.2.4) it follows that all odd moments of the normal distribution are equal to zero. This, however, directly follows from the symmetry of the normal law.

For even The following expressions for consecutive moments are derived from formula (6.2.4):

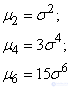
etc.

General formula for the moment th order for any even has the form:

,

where under the symbol 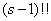understood the product of all odd numbers from 1 to .

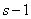So as for normal law 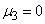, its asymmetry is also zero:

.

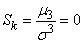From the expression of the fourth moment

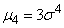
we have:

,

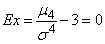those. the excess of normal distribution is zero. This is only natural, since the purpose of an excess is to characterize the relative steepness of this law as compared to normal.