16.3. Linear transformations of random functions defined by canonical decompositions

Let the input of some linear system random function arrives 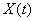(fig. 16.3.1).

Fig. 16.3.1.

The system converts the function 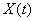by means of a linear operator and at the output we get a random function

. (16.3.1)

Suppose a random function 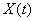given by its canonical decomposition:

. (16.3.2)

We determine the response of the system to this effect. Since the system operator is linear,

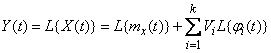. (16.3.3)

Considering the expression (16.3.3), it is easy to verify that it represents nothing more than a canonical decomposition of a random function with mathematical expectation

(16.3.4)

and coordinate functions

. (16.3.5)

Thus, in the linear transformation of the canonical expansion of a random function canonical decomposition of a random function is obtained 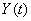, and the mean and coordinate functions undergo the same linear transformation.

If random function 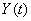at the output of the linear system obtained in the form of canonical decomposition

, (16.3.6)

then its correlation function and variance are quite simple:

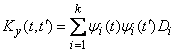, (16.3.7)

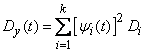. (16.3.8)

This makes it particularly convenient canonical expansions compared to any other decompositions in elementary functions.

Let us consider in more detail the application of the method of canonical expansions to the definition of the reaction of a dynamical system to a random input action, when the operation of the system is described by a linear differential equation, in the general case with variable coefficients. We write this equation in operator form:

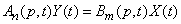. (16.3.9)

According to the above rules of linear transformations of random functions, the expectation of exposure and reaction must satisfy the same equation:

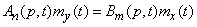. (3/16/10)

Similarly, each of the coordinate functions must satisfy the same differential equation:

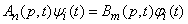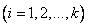, . (3/16/11)

Thus, the problem of determining the response of a linear dynamic system to a random effect has been reduced to the usual mathematical problem of integration ordinary differential equations containing ordinary, non-random functions. Since, when solving the basic problem of analyzing a dynamic system — determining its response to a given effect — is the task of integrating a differential equation that describes the operation of the system, it is solved in one way or another, when solving equations (16.3.10) and (16.3.11) new mathematical difficulties does not occur. In particular, the same integrating systems or modeling devices that are used to analyze the operation of the system without random perturbations can be successfully applied to solve these equations.

It remains to clarify the question of the initial conditions under which equations (16.3.10) and (16.3.11) should be integrated.

First, we consider the simplest case when the initial conditions for a given dynamical system are nonrandom. In this case, when 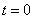conditions must be met:

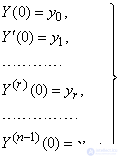(3/16/12)

Where - non-random numbers.

Conditions (16.3.12) can be written more compactly:

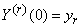
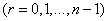(16.3.13)

understanding the term “derivative of zero order” 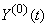the function itself .

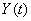Let us find out under what initial conditions the equations (16.3.10) and (16.3.11) should be integrated. For this we find 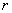derivative of the function 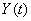and put in it :

.

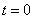Considering (16.3.12), we have:

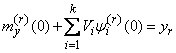. (3/16/14)

Since the value 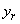not random, the variance of the left side of equality (16.3.14) should be zero:

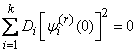. (3/16/15)

Since all dispersions 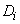values are positive, then equality (16.3.15) can be realized only when

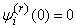(3/16/16)

for all .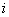

Substituting 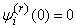in the formula (16.3.14), we get:

. (16.3.17)

From equality (16.3.17) it follows that the equation (16.3.10) for the expectation must be integrated under the given initial conditions (16.3.12):

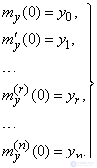(3/16/18)

As for equations (16.3.11), they should be integrated with zero initial conditions:

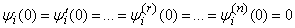
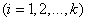. (3/16/19)

Consider a more complicated case when the initial conditions are random:

(3/16/20)

Where 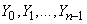- random variables.

In this case, the response at the output of the system can be found as a sum:

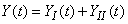, (16.3.21)

Where 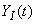- solution of the differential equation (16.3.9) with zero initial conditions; 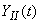- the solution of the same differential equation, but with a zero right-hand side under given initial conditions (16.3.20). As is known from the theory of differential equations, this solution is a linear combination of initial conditions:

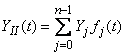, (16.3.22)

Where - non-random functions.

Decision 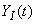can be obtained by the above method in the form of canonical decomposition. Correlation function of a random function 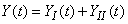can be found by the usual methods of adding random functions (see 15.8).

It should be noted that in practice there are very often cases where, for moments of time sufficiently distant from the beginning of the random process, the initial conditions no longer affect its flow: the transients caused by them have time to die out. Systems with this property are called asymptotically stable. If we are interested in the reaction of an asymptotically stable dynamical system on time intervals sufficiently distant from the beginning, then we can restrict ourselves to studying the solution 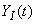obtained with zero initial conditions. For sufficiently remote from the initial moments of time, this solution will be valid under any initial conditions.