Lecture
Probability theory is a mathematical science that studies patterns in random phenomena.
We agree on what we will mean by "accidental occurrence."
In the scientific study of various physical and technical problems one often has to meet with a special type of phenomena, which are commonly called random. An accidental phenomenon is a phenomenon that, with repeated reproduction of the same experience, proceeds somewhat differently each time.
We give examples of random phenomena.
1. Shooting from a gun mounted at a given angle to the horizon (Fig. 1.1.1).
Using the methods of external ballistics (the science of the movement of the projectile in the air), you can find the theoretical trajectory of the projectile (curve 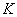 in fig. 1.1.1). This trajectory is completely determined by the shooting conditions: the initial velocity of the projectile
in fig. 1.1.1). This trajectory is completely determined by the shooting conditions: the initial velocity of the projectile 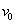 throwing angle
throwing angle  and ballistic coefficient of the projectile
and ballistic coefficient of the projectile 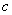 . The actual trajectory of each individual projectile inevitably deviates somewhat from the theoretical due to the cumulative effect of many factors. Among these factors you can, for example, call the following: the manufacture of the projectile, the deviation of the charge weight from the nominal, the heterogeneity of the charge structure, the installation error of the barrel in a given position, meteorological conditions, etc. If you make several shots under the same basic conditions (
. The actual trajectory of each individual projectile inevitably deviates somewhat from the theoretical due to the cumulative effect of many factors. Among these factors you can, for example, call the following: the manufacture of the projectile, the deviation of the charge weight from the nominal, the heterogeneity of the charge structure, the installation error of the barrel in a given position, meteorological conditions, etc. If you make several shots under the same basic conditions ( 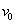 ,
,  ,
, 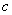 ), we get not a single theoretical trajectory, but a whole bunch or “sheaf” of trajectories that form the so-called “projectile dispersion”.
), we get not a single theoretical trajectory, but a whole bunch or “sheaf” of trajectories that form the so-called “projectile dispersion”.

Fig. 1.1.1.
2. The same body is weighed several times on an analytical balance; the results of repeated weighing are somewhat different from each other. These differences are due to the influence of many minor factors accompanying the weighing operation, such as body position on the scale pan, random equipment vibrations, instrument readout errors, etc.
3. The aircraft flies at a given altitude; theoretically it flies horizontally, evenly and straightforwardly. In fact, the flight is accompanied by deviations of the center of mass of the aircraft from the theoretical trajectory and oscillations of the aircraft near the center of mass. These deviations and vibrations are random and are associated with the turbulence of the atmosphere; from time to time they do not repeat.
4. A number of explosions of fragmentation projectile are carried out in a certain position relative to the target. The results of individual explosions are somewhat different from each other: the total number of fragments, the relative position of their trajectories, the weight, shape, and speed of each individual fragment vary. These changes are random and are related to the influence of such factors as the heterogeneity of the metal of the projectile body, the heterogeneity of the explosive, the inconstancy of the detonation velocity, etc. In this regard, various explosions carried out, seemingly under the same conditions, can lead to different results: in some explosions, the target will be hit by fragments, in others it will not.
All these examples are considered here from the same angle of view: random variations are emphasized, the unequal results of a number of experiments, the basic conditions of which remain unchanged. These variations are always associated with the presence of some minor factors affecting the outcome of the experiment, but not specified in the number of its basic conditions. The basic conditions of experience, which determine its course in general and coarse terms, remain unchanged; secondary - vary from experience to experience and introduce random differences in their results.
It is quite obvious that in nature there is not a single physical phenomenon in which elements of randomness are not present in one degree or another. No matter how accurately and in detail the conditions of experience were fixed, it is impossible to achieve that with the repetition of experience, the results completely and exactly coincide.
Random deviations inevitably accompany any natural phenomenon. Nevertheless, in a number of practical tasks these random elements can be neglected, considering instead of the real phenomenon its simplified scheme, the “model”, and assuming that under the given conditions of experience the phenomenon proceeds in a very definite way. At the same time, out of an infinite number of factors influencing this phenomenon, the most important, main, decisive ones are distinguished; the influence of other, secondary factors is simply neglected. Such a scheme for studying phenomena is constantly used in physics, mechanics, and technology. When using this scheme to solve any problem, first of all, the main range of conditions taken into account is identified and it becomes clear what parameters of the problem they influence; then one or another mathematical apparatus is applied (for example, differential equations describing the phenomenon are compiled and integrated); thus, the main regularity inherent in this phenomenon and giving the opportunity to predict the result of the experiment according to its given conditions is revealed. As science develops, the number of factors taken into account becomes more and more; the phenomenon is investigated in more detail; scientific forecast becomes more accurate.
However, for solving a number of issues, the described scheme - the classical scheme of the so-called “exact sciences” - turns out to be poorly adapted. There are problems where the outcome of the experiment that interests us depends on so many factors that it is almost impossible to register and take into account all these factors. These are tasks in which numerous minor, closely intertwined random factors play a noticeable role, and at the same time their number is so great and the influence is so complex that the use of classical research methods does not justify itself.

Fig. 1.1.2.
Consider an example. Shooting at some target C from a gun mounted at an angle  to the horizon (Fig. 1.1.2). The trajectories of the shells, as mentioned above, do not coincide with each other; as a result, the shells fall on the ground. If the dimensions of the target are large compared to the area of dispersion, then this dispersion can obviously be neglected: if the cannon is correctly installed, any projectile fired hits the target. If (as is usually the case in practice) the area of dispersion of shells exceeds the size of the target, then some of the projectiles will not hit the target due to the influence of random factors. A number of questions arise, for example: on average, what percentage of shells hit the target? How many shells need to spend in order to hit the target reliably enough? What measures should be taken to reduce the consumption of shells?
to the horizon (Fig. 1.1.2). The trajectories of the shells, as mentioned above, do not coincide with each other; as a result, the shells fall on the ground. If the dimensions of the target are large compared to the area of dispersion, then this dispersion can obviously be neglected: if the cannon is correctly installed, any projectile fired hits the target. If (as is usually the case in practice) the area of dispersion of shells exceeds the size of the target, then some of the projectiles will not hit the target due to the influence of random factors. A number of questions arise, for example: on average, what percentage of shells hit the target? How many shells need to spend in order to hit the target reliably enough? What measures should be taken to reduce the consumption of shells?
In order to answer such questions, the ordinary exact sciences scheme is not enough. These issues are organically linked to the random nature of the phenomenon; in order to answer them, obviously, one cannot simply neglect randomness — it is necessary to study the random phenomenon of the dispersion of projectiles from the point of view of the laws inherent in it just as a random phenomenon. It is necessary to investigate the law according to which the points of falling of shells are distributed; you need to figure out random causes of dispersion, compare them with each other in order of importance, etc.
Consider another example. Some technical device, for example, an automatic control system, solves a certain problem in conditions when random noise interferes with the system continuously. The presence of interference leads to the fact that the system solves the problem with some error, in some cases beyond the permissible limits. The questions arise: how often will such errors appear? What measures should be taken in order to virtually eliminate their possibility?
In order to answer such questions, it is necessary to investigate the nature and structure of random perturbations affecting the system, study the system response to such perturbations, and determine the influence of the system’s design parameters on the appearance of this reaction.
All such tasks, the number of which in physics and technology is extremely large, require the study of not only the main, main laws that determine the phenomenon in general, but also the analysis of random perturbations and distortions associated with the presence of secondary factors and giving the outcome of experience under given conditions an element of uncertainty .
What are the ways and methods for the study of random phenomena?
From a purely theoretical point of view, the factors that we conditionally called "random" factors, in principle, are no different from others, which we have identified as "basic". Theoretically, it is possible to unlimitedly increase the accuracy of solving each task, taking into account more and more new groups of factors: from the most essential to the most insignificant. However, in practice, such an attempt to analyze the influence of resolutely all the factors on which the phenomenon depended would be equally detailed and would only lead to the fact that the solution of the problem, because of its excessive bulkiness and complexity, would be practically impracticable and, moreover, would have no cognitive value. .
For example, theoretically it would be possible to pose and solve the problem b of determining the trajectory of a well-defined projectile, taking into account all the specific errors of its manufacture, the exact weight and the specific structure of a given, well-defined powder charge with precisely defined meteorological data (temperature, pressure, humidity, wind) at each point of the trajectory. Such a decision would not only be immensely difficult, but would also have no practical value, since it would apply only to this particular projectile and charge in these specific conditions, which will practically not be repeated.
Obviously, there should be a fundamental difference in the methods of accounting for the main, decisive factors, which determine in the main features the course of the phenomenon, and secondary, minor factors that influence the course of the phenomenon as “errors” or “disturbances”. The element of uncertainty, complexity, and multi-causality inherent in random phenomena requires the creation of special methods for studying these phenomena.
Such methods are developed in the theory of probability. Its subject is specific patterns observed in random phenomena.
Practice shows that, by observing together the masses of homogeneous random phenomena, we usually find in them quite definite patterns, a kind of stability, peculiar to mass random phenomena.
For example, if you repeatedly throw a coin, the frequency of the emblem (the ratio of the number of emblems that appeared to the total number of throws) gradually stabilizes, approaching a well-defined number, namely, to ½. The same property of “frequency stability” is also found with repeated repetition of any other experience, the outcome of which appears to be uncertain beforehand, random. So, with an increase in the number of shots, the frequency of hitting a certain target also stabilizes, approaching a certain constant number.
Consider another example. There is a volume of gas in the vessel, consisting of a very large number of molecules. Each molecule in a second experiences many collisions with other molecules, repeatedly changes the speed and direction of movement; the trajectory of each individual molecule is random. It is known that the pressure of a gas on a vessel wall is caused by a combination of molecular impacts on this wall. It would seem that if the trajectory of each individual molecule is random, then the pressure on the vessel wall would have to change in a random and uncontrolled manner; However, it is not. If the number of molecules is sufficiently large, then the gas pressure practically does not depend on the trajectories of individual molecules and obeys a well-defined and very simple pattern. The random features inherent in the movement of each individual molecule are mutually compensated in the mass; as a result, despite the complexity and entanglement of a separate random phenomenon, we get a very simple pattern, valid for a mass of random phenomena. We note that it is precisely the mass character of random phenomena that ensures the fulfillment of this regularity; with a limited number of molecules, random deviations from regularities, the so-called fluctuations, begin to appear.
Consider another example. At some target, one after another series of shots is fired; there is a distribution of hit points on the target. With a limited number of shots, the points of impact are distributed across the target in complete disarray, without any visible pattern. As the number of shots increases, some regularity begins to be observed in the location of points; this pattern is manifested the more clearly, the greater the number of shots made. The location of the points of impact turns out to be approximately symmetrical with respect to some central point: in the central region of the group of holes they are located thicker than at the edges; at the same time, the density of holes decreases according to a well-defined law (the so-called “normal law” or “Gauss law”, which will receive much attention in this course).
Such specific, so-called “statistical” laws are always observed when we are dealing with a mass of homogeneous random phenomena. The patterns that manifest themselves in this mass turn out to be practically independent of the individual characteristics of individual random phenomena belonging to the mass. These individual features in the mass seem to be mutually extinguished, leveled out, and the average result of the mass of random phenomena turns out to be practically not random. It is this stability, confirmed many times by experience, of mass random phenomena that serves as the basis for applying probabilistic (statistical) research methods. The methods of probability theory are by their nature adapted only for the study of mass random phenomena; they do not make it possible to predict the outcome of a single random phenomenon, but they make it possible to predict the average total result of a mass of homogeneous random phenomena, to predict the average outcome of a mass of similar experiments, the specific outcome of each of which remains uncertain, random.
The greater the number of homogeneous random phenomena involved in the task, the more clearly and distinctly the specific laws inherent in them appear, the more confident and accurate can be the scientific prediction.
In all cases when probabilistic research methods are used, their purpose is to bypass too complex (and often practically impossible) study of a separate phenomenon, caused by too many factors, directly to the laws governing the masses of random phenomena. The study of these laws allows not only to carry out a scientific forecast in a peculiar area of random phenomena, but in some cases it helps to purposefully influence the course of random phenomena, control them, limit the scope of randomness, and narrow its influence on practice.
The probabilistic, or statistical, method in science does not oppose itself to the classical, ordinary method of the exact sciences, but is its supplement, which allows for a deeper analysis of the phenomenon taking into account its inherent elements of randomness.
A very wide and fruitful application of statistical methods in all fields of knowledge is characteristic of the modern stage of development of the natural and technical sciences. This is quite natural, since the in-depth study of any circle of phenomena inevitably comes a stage when not only the identification of the basic laws, but also the analysis of possible deviations from them is required. In some sciences, due to the specificity of the subject and historical conditions, the introduction of statistical methods is observed earlier, in others - later. Currently, there is almost no natural science in which, one way or another, probabilistic methods would not be applied. Entire sections of modern physics (in particular, nuclear physics) are based on the methods of probability theory. Probabilistic methods are increasingly being used in modern electrical engineering, radio engineering, meteorology and astronomy, the theory of automatic control, and computer mathematics.
The field of applications is widely used in various fields of military technology: the theory of firing and bombing, the theory of ammunition, the theory of scopes and fire control devices, air navigation, tactics and many other branches of military science are widely used methods of probability theory and its mathematical apparatus.
The mathematical laws of probability theory are a reflection of real statistical laws that objectively exist in mass random phenomena of nature. To the study of these phenomena, probability theory applies the mathematical method and is in its method one of the branches of mathematics that is as logically accurate and rigorous as other mathematical sciences.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis