9.2 Ellipses of dispersion. Reduction of the normal law to canonical form

Consider the surface distribution, depicting the function (9.1.1). It looks like a hill, the top of which is above the point 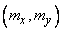(fig. 9.2.1).

In the cross section of the surface of the distribution planes parallel to the axis 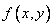, we get curves similar to normal distribution curves. In the cross section of the surface of the distribution planes parallel to the plane 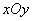, ellipses are obtained. We write the equation of the projection of such an ellipse on the plane :

,

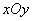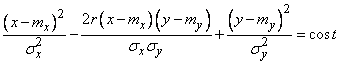or denoting a constant ,

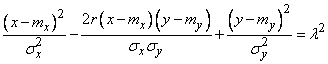. (9.2.1)

The equation of the ellipse (9.2.1) can be analyzed by conventional methods of analytic geometry. Applying them, we make sure that the center of the ellipse (9.2.1) is at the point with coordinates 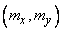; as for the direction of the axes of symmetry of the ellipse, then they make up with the axis equation angles

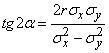. (9.2.2)

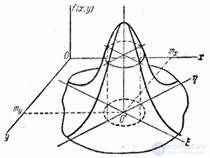
Fig. 9.2.1

This equation gives two angles: 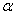and 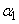differing by .

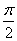Thus, the orientation of the ellipse (9.2.1) relative to the coordinate axes is directly dependent on the correlation coefficient 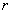systems 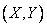; if the values ​​are not correlated (that is, in this case they are independent), then the symmetry axes of the ellipse are parallel to the coordinate axes; otherwise, they make an angle with the coordinate axes.

Intersecting the distribution surface with planes parallel to the plane 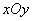and designing sections on the plane 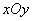we will get a whole family of similar and equally spaced ellipses with a common center 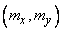. At all points of each of these ellipses, the distribution density 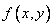is constant. Therefore, such ellipses are called ellipses of equal density or, in short, ellipses of dispersion. The common axes of all ellipses of dispersion are called the main axes of dispersion.

It is known that the equation of an ellipse takes the most simple, so-called "canonical" form, if the coordinate axes coincide with the axes of symmetry of the ellipse. In order to bring the scattering ellipse equation to the canonical form, it is sufficient to transfer the origin to the point 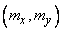and rotate the coordinate axes by an angle 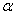defined by equation (9.2.2). In this case, the coordinate axes coincide with the main axes of dispersion, and the normal law on the plane is converted to the so-called "canonical" form.

The canonical form of the normal law on the plane has the form

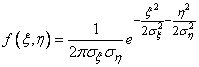, (9.2.3)

Where - the so-called main standard quadratic deviations, i.e. mean square deviations of random variables 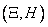that represent the coordinates of a random point in the coordinate system defined by the main scatter axes 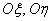. Main average quadratic deviations 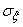and 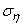expressed in terms of standard deviations in the previous coordinate system by the formulas:

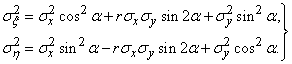(9.2.4)

Usually, considering the normal law on the plane, try to pre-select the coordinate axes so that they coincide with the main axes of dispersion. In this case, the standard deviations of the axes 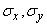and will be the main standard deviations, and the normal law will be:

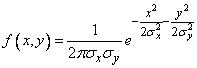. (9.2.5)

In some cases, the coordinate axes are chosen parallel to the main dispersion axes, but the origin of coordinates is not aligned with the center of dispersion. Moreover, random variables 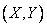also turn out to be independent, but the expression of a normal law is:

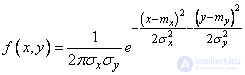, (9.2.6)

Where 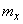and 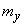- coordinates of the center of dispersion.

Let us proceed in the canonical form of the normal law (9.2.5) from the standard deviations to the probable deviations:

.

Values 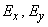are called the main probable deviations. Substituting expressions 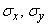through 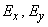in equation (9.2.5), we obtain another canonical form of the normal law:

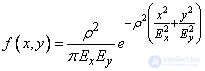. (9.2.7)

In this form, the normal law is often applied in the theory of shooting.

We write the equation of the dispersion ellipse in canonical form:

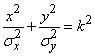or 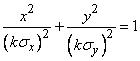. (9.2.8)

Where 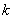- constant number.

From the equation it can be seen that the semi-axes of the dispersion ellipse are proportional to the principal mean square deviations (and, therefore, to the main probable deviations).

Let us call the “unit” ellipse of dispersion the one of the ellipses of equal probability density, whose semi-axes are equal to the principal mean square deviations 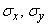. (If the scattering characteristics are not the main mean square, but the main probable deviations, then it is natural to call an “ellipse” the ellipse whose semi-axes are equal ).

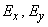In addition to a single ellipse of dispersion, sometimes they also consider the “full” ellipse of dispersion, which is understood to be that of ellipses of equal probability density, in which all dispersion fits with practical certainty. The dimensions of this ellipse, of course, depend on what is meant by “practical certainty”. In particular, if we take the probability of the order of 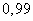then the “full scattering ellipse” can be considered an ellipse with semi-axes .

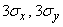Let us consider specifically one particular case when the main standard deviations are equal to each other:

.

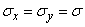Then all the ellipses of dispersion turn into circles, and the dispersion is called circular. With circular dispersion, each of the axes passing through the center of dispersion can be taken for the main axis of dispersion, or, in other words, the direction of the main axes of dispersion is uncertain. With non-circular scatter random values 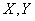subordinate to the normal law on the plane, are independent if and only if the coordinate axes are parallel to the main axes of dispersion; with circular dispersion random variables 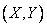independent of any choice of rectangular coordinate system. This feature of circular scattering leads to the fact that it is much more convenient to operate with circular scattering than with elliptical scattering. Therefore, in practice, wherever possible, they strive to replace the non-circular dispersion with a circular one.