Lecture
The particular theorem on repetition of experiments concerns the case when the probability of an event 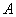 in all experiments is the same. In practice, one often encounters a more complex case, when experiments are carried out in different conditions, and the probability of an event varies from experience to experience. For example, if a series of shots are made in varying conditions (for example, with varying range), then the probability of hitting from shot to shot may change noticeably.
in all experiments is the same. In practice, one often encounters a more complex case, when experiments are carried out in different conditions, and the probability of an event varies from experience to experience. For example, if a series of shots are made in varying conditions (for example, with varying range), then the probability of hitting from shot to shot may change noticeably.
The method of calculating the probability of a given number of occurrences of an event in such conditions gives a general theorem on the repetition of experiments.
Let n independent experiments be performed, in each of which some event may or may not appear. 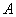 , with the probability of occurrence
, with the probability of occurrence 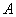 in i-th experience is equal
in i-th experience is equal 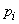 and the probability of non-occurrence
and the probability of non-occurrence 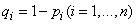 . Required to find the probability
. Required to find the probability  that as a result
that as a result 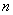 experiences event
experiences event 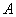 will appear exactly
will appear exactly  time.
time.
Denote as before  event consisting in that event
event consisting in that event 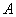 will appear
will appear  once in
once in 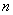 experiences. Still imagine
experiences. Still imagine  as the sum of the products of elementary events:
as the sum of the products of elementary events:
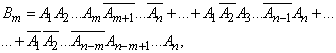
and in each of the works of the event 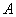 enters
enters  time event
time event 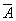 -
- 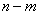 time. The number of such combinations will still be
time. The number of such combinations will still be 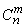 , but the combinations themselves will be already unequal.
, but the combinations themselves will be already unequal.
Applying the addition theorem and the multiplication theorem for independent events, we obtain:
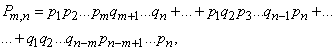
those. the required probability is equal to the sum of all possible products in which the letters 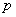 with different indexes are included
with different indexes are included  times and letters
times and letters 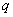 with different indexes
with different indexes 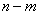 time.
time.
In order to mechanically compose all possible works from  letters
letters 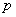 and
and 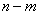 letters
letters 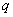 with different indices, apply the following formal method. We make the product
with different indices, apply the following formal method. We make the product 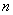 binomials:
binomials:
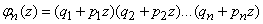
or shorter
 ,
,
Where 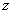 - arbitrary parameter.
- arbitrary parameter.
Let us set ourselves the goal of finding in this product of binomials a coefficient with 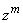 . To do this, multiply the binomials and produce a cast of such terms. Obviously, every member containing
. To do this, multiply the binomials and produce a cast of such terms. Obviously, every member containing 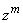 , will have as a coefficient the product
, will have as a coefficient the product  letters
letters 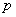 with some indices and
with some indices and 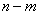 letters
letters 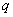 and after bringing such members into account
and after bringing such members into account 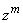 will be the sum of all possible works of this type. Consequently, the method of compiling this coefficient completely coincides with the method of calculating the probability
will be the sum of all possible works of this type. Consequently, the method of compiling this coefficient completely coincides with the method of calculating the probability  in the problem of repeating experiments.
in the problem of repeating experiments.
Function 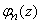 whose decomposition is in powers of the parameter
whose decomposition is in powers of the parameter 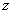 gives probability coefficients
gives probability coefficients  , is called the generating probability function
, is called the generating probability function  , or simply generating function.
, or simply generating function.
Using the concept of a generating function, we can formulate a theorem on the repetition of experiments in the following form.
Probability that an event 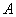 at
at 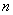 independent experiences will appear exactly
independent experiences will appear exactly  times equal to the coefficient at
times equal to the coefficient at 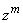 in the expression of the generating function:
in the expression of the generating function:
 ,
,
Where 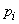 - probability of occurrence
- probability of occurrence 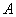 in the i-th experience
in the i-th experience 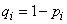 .
.
The above formulation of the general theorem on the repetition of experiments, in contrast to the particular theorem, does not give an explicit expression for the probability  . Such an expression, in principle, can be written, but it is too complex, and we will not give it. However, without resorting to such an explicit expression, it is still possible to write the general theorem on the repetition of experiments in the form of one formula:
. Such an expression, in principle, can be written, but it is too complex, and we will not give it. However, without resorting to such an explicit expression, it is still possible to write the general theorem on the repetition of experiments in the form of one formula:
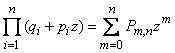 . (4.2.1)
. (4.2.1)
The left and right sides of equality (4.2.1) are the same generating function. 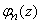 , only to the left it is written as a monomial, and to the right - as a polynomial. Opening the brackets on the left side and performing the cast of such terms, we get all the probabilities:
, only to the left it is written as a monomial, and to the right - as a polynomial. Opening the brackets on the left side and performing the cast of such terms, we get all the probabilities:
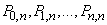
as coefficients, respectively, at zero, first, etc. degrees 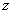 .
.
Obviously, the particular theorem on the repetition of experiments follows from the general at
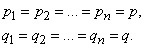
In this case, the generating function refers to 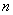 degree of binomial
degree of binomial 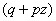 :
:
 .
.
Opening this expression according to the formula of the binomial, we have:
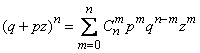 ,
,
whence formula (4.1.1) follows.
Note that, both in general and in the particular case, the sum of all probabilities  equals one:
equals one:
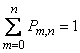 . (4.2.2)
. (4.2.2)
This follows, first of all, from the fact that events 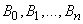 form a complete group of incompatible events. Formally, equality (4.2.2) can be achieved by assuming in the general formula (4.2.1)
form a complete group of incompatible events. Formally, equality (4.2.2) can be achieved by assuming in the general formula (4.2.1) 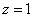 .
.
In many cases, the practice, besides the probability  smooth
smooth  occurrences of event A, we must consider the probability of not less than
occurrences of event A, we must consider the probability of not less than  occurrences of the event A.
occurrences of the event A.
Denote 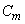 an event consisting in that event A appears at least
an event consisting in that event A appears at least  times, and the probability of an event
times, and the probability of an event 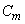 denote
denote 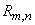 . Obviously
. Obviously
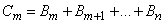 ,
,
from which, by the addition theorem,
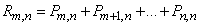 ,
,
or shorter
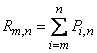 . (4.2.3)
. (4.2.3)
When calculating 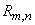 it is often more convenient not to use directly the formula (4.2.3), but to go to the opposite event and calculate the probability
it is often more convenient not to use directly the formula (4.2.3), but to go to the opposite event and calculate the probability 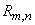 according to the formula
according to the formula
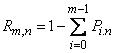 . (4.2.4)
. (4.2.4)
Example 1. 4 independent shots are fired at the same target from different distances; the probabilities of hitting with these shots are respectively
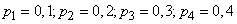 .
.
Find the probabilities of no, one, two, three, or four hits:
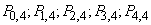 .
.
Decision. We make the generating function:
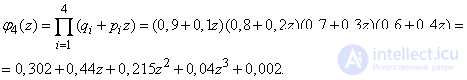
from where
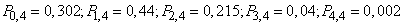 .
.
Example 2. 4 independent shots are made under the same conditions, and the probability of hitting p is the average of the probabilities 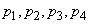 previous example:
previous example:
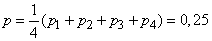 .
.
Find probabilities
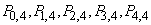 .
.
Decision. By the formula (4.1.1) we have:

Example 3. There are 5 stations with which communication is supported. From time to time the connection is interrupted due to atmospheric noise. Due to the distance of the stations from each other, the interruption of communication with each of them occurs independently of the others with a probability  . Find the probability that at a given time there is a connection with no more than two stations.
. Find the probability that at a given time there is a connection with no more than two stations.
Decision. The event in question, is reduced to the fact that communication will be broken no less than the stirrup stations. By the formula (4.2.3) we get:
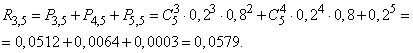
Example 4. A system of radar stations monitors a group of objects consisting of 10 units. Each of the objects can be (independently of the others) lost with a probability of 0.1. find the probability that at least one of the objects will be lost.
Decision. The probability of losing at least one object 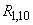 could be found by the formula
could be found by the formula
 ,
,
but it is much easier to use the probability of the opposite event - not a single object is lost - and subtract it from one:
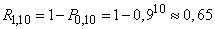 .
.
Example 5. The device consists of 8 homogeneous elements, but can work in the presence in good condition of at least 6 of them. Each of the elements during the operation of the device 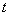 fails independently of others with a probability of 0.2. Find the probability that the device fails in time.
fails independently of others with a probability of 0.2. Find the probability that the device fails in time. 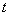 .
.
Decision. For failure of the device requires the failure of at least two of the eight elements. By the formula (4.2.4) we have:
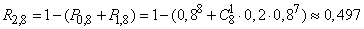 .
.
Example 6. There are 4 independent shots from the aircraft on the aircraft. The probability of hitting each shot is 0.3. For defeat (failure) of the plane, two hits are known to be sufficient; with one plane is hit with a probability of 0.6. Find the probability that the plane will be hit.
Decision. The problem is solved by the formula of total probability. Hypotheses could be considered.
 - 1 projectile hit the plane,
- 1 projectile hit the plane,
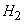 - 2 missiles hit the plane,
- 2 missiles hit the plane,
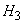 - 3 missiles hit the plane,
- 3 missiles hit the plane,
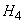 - 4 missiles hit the plane
- 4 missiles hit the plane
and to find the probability of an A event - the destruction of an aircraft - using these four hypotheses. However, it is much easier to consider only two hypotheses:
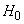 - not a single shell hit the plane,
- not a single shell hit the plane,
 - 1 projectile hit the plane,
- 1 projectile hit the plane,
and calculate the probability of an event 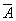 - non-impact aircraft:
- non-impact aircraft:
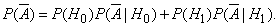
We have:

Consequently,
 ,
,
from where
 .
.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis