9.5. Probability of hitting an area of ​​arbitrary shape

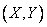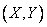When firing projectiles, calculating the probability of hitting the target is reduced to calculating the probability of hitting a random point in some area . Let random point subject to normal law in canonical form. Probability of hitting a point 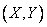to the area 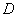expressed by the integral

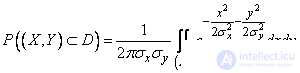. (9.5.1)

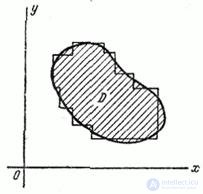
Fig. 9.5.1

In some particular cases (for example, when 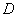there is a rectangle with sides parallel to the main axes of dispersion, or an ellipse of dispersion, as well as in some others that have less practical value) the integral (9.5.1) can be expressed through known functions; in the general case, this integral is not expressed through known functions. In practice, the following approximate methods are used to calculate the probability of hitting an area of ​​arbitrary shape.

1. Area 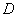approximately replaced by an area made up of rectangles whose sides are parallel to the main dispersion axes (Fig.9.5.1). The probability of hitting each of these rectangles is calculated by the formula (9.3.3). This method can be recommended when the number of rectangles into which the target is approximately broken. 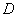, not too large.

2. The whole plane 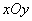With the help of a certain system of lines (straight lines or curves), it is pre-divided into a series of cells, the probabilities of entering which can be expressed precisely through known functions, and the probability of falling into each cell is calculated. Such a system of lines with corresponding probabilities of hitting the cells is called a dispersion grid. Working with the grid is that the image of the grid is superimposed on the image of the target, after which the probabilities of hitting the cells covered with the target are summed up; if the target covers a part of the cell, then the part of the probability of hitting the cell is taken, which is proportional to the covered area.

The scattering grid can be applied in two ways: a) build a target at the grid scale, b) build a grid at the target scale.

If the goal has complex outlines and, especially, if it is relatively small, it is usually more convenient to construct on the image of the target on the same scale that part of the grid that is occupied by the target. If the target has a relatively simple shape and is quite large (occupies a significant part of the full ellipse of dispersion), it is usually more convenient to build a target at the grid scale. Since the standard grid is built for circular scattering, and in practice, scattering is generally not circular, when building a goal on a grid scale, it is generally necessary to use two different scales along the axes 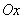and 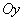. With this method, it is convenient to have a scattering grid, made on transparent paper, and overlay it on the rearranged image of the target. The rectilinear scattering grid for one coordinate angle is given in Fig. 9.5.2. Cell side is equal to .

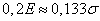Fig. 9.5.2

The cells bear the probabilities of hitting them, expressed in the fortieth fractions of a percent.

1. In the case where the dimensions of the area 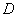small compared with the standard deviations (do not exceed s.k.o. in the direction of the corresponding axes), the probability of hitting this area can be approximately calculated by a formula that does not contain an integration operation.

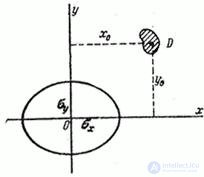
Fig. 9.5.3

Consider on the plane 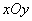small target 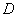arbitrary shape (Fig. 9.5.3). Assume that the size of this goal is small compared with the probable deviations 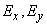. According to the general formula (8.3.3) we have:

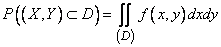. (9.5.2)

Where 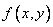- system distribution density 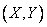. Apply to integral (9.5.2) the mean value theorem:

,

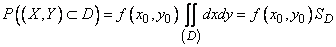Where 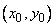- some point inside the area 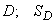- area of ​​the region .

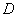In the case where the system 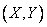subordinated to the normal law in the canonical form, we have:

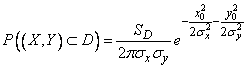. (9.5.3)

With a relatively small area 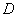distribution density 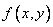within this region changes little and can practically be taken constant. Then as a point 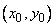you can select any point within the area 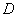(for example, approximate target center).

Formulas like (9.5.3) are widely used in practice. For areas whose largest dimensions do not exceed 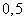standard deviations in the corresponding direction, they give quite acceptable accuracy results. In some cases, they are also used for larger areas (of the order of one sko). Subject to some amendments (namely, the replacement of 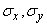slightly increased values) the range of applicability of this formula can be extended to areas of the order of two sk. sizes.