Lecture
Different forms of the central limit theorem differ among themselves by the conditions imposed on the distributions forming the sum of random terms. Here we formulate and prove one of the simplest forms of the central limit theorem, which refers to the case of identically distributed terms.
Theorem. If a 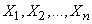 - independent random variables having the same distribution law with the expectation
- independent random variables having the same distribution law with the expectation 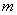 and variance
and variance 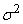 , then with an unlimited increase
, then with an unlimited increase 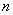 amount distribution law
amount distribution law
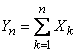 (13.8.1)
(13.8.1)
unlimited approaches to normal.
Evidence.
We will carry out the proof for the case of continuous random variables.  (for discontinuous it will be similar).
(for discontinuous it will be similar).
According to the second property of the characteristic functions, proved in the previous  , characteristic function of magnitude
, characteristic function of magnitude 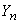 is a product of the characteristic functions of the terms. Random variables
is a product of the characteristic functions of the terms. Random variables 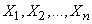 have the same distribution law with density
have the same distribution law with density 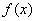 and therefore the same characteristic function
and therefore the same characteristic function
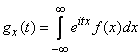 . (13.8.2)
. (13.8.2)
Therefore, the characteristic function of a random variable 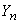 will be
will be
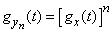 . (13.8.3)
. (13.8.3)
We investigate in more detail the function  . Imagine it in a neighborhood of a point.
. Imagine it in a neighborhood of a point. 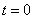 according to the Maclaurin formula with three members:
according to the Maclaurin formula with three members:
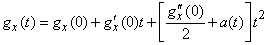 , (13.8.4)
, (13.8.4)
Where 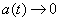 at
at 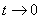 .
.
Find the values 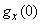 ,
,  ,
, 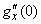 . Assuming in the formula (13.8.2)
. Assuming in the formula (13.8.2) 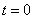 we have:
we have:
 . (13.8.5)
. (13.8.5)
Differentiate (13.8.2) by 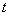 :
:
 . (13.8.6)
. (13.8.6)
Putting in (13.8.6) 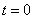 , we get:
, we get:
 . (13.8.7)
. (13.8.7)
Obviously, without limiting the generality, you can put 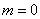 (for this it is enough to move the origin to the point
(for this it is enough to move the origin to the point 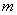 ). Then
). Then
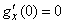 .
.
Let's differentiate (13.8.6) again:
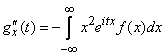 ,
,
from here
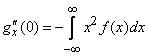 . (13.8.8)
. (13.8.8)
With 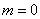 the integral in expression (13.8.8) is nothing but the dispersion of the quantity
the integral in expression (13.8.8) is nothing but the dispersion of the quantity 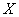 with density
with density 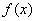 , Consequently
, Consequently
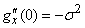 . (13.8.9)
. (13.8.9)
Substituting in (13.8.4) 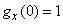 ,
, 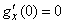 and
and 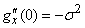 , we get:
, we get:
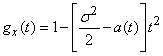 . (13.8.10)
. (13.8.10)
Let's turn to random  . We want to prove that its distribution law with increasing
. We want to prove that its distribution law with increasing 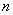 approaching normal. To do this, move on from
approaching normal. To do this, move on from 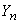 to another ("normalized") random value
to another ("normalized") random value
 . (13.8.11)
. (13.8.11)
This value is convenient because its dispersion does not depend on 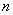 and is equal to one for any
and is equal to one for any 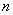 . It is easy to verify this, considering the value
. It is easy to verify this, considering the value 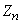 as a linear function of independent random variables
as a linear function of independent random variables 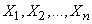 each of which has a variance
each of which has a variance 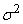 . If we prove that the distribution law
. If we prove that the distribution law 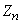 approaching normal, then obviously it will be true for the magnitude
approaching normal, then obviously it will be true for the magnitude 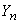 associated with
associated with 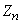 linear dependence (13.8.11).
linear dependence (13.8.11).
Instead of proving that the distribution law 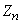 while increasing
while increasing 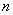 approaches normal, we show that its characteristic function approaches the characteristic function of a normal law.
approaches normal, we show that its characteristic function approaches the characteristic function of a normal law.
Find the characteristic function of 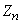 . From relation (13.8.11), according to the first property of the characteristic functions (13.7.8), we obtain
. From relation (13.8.11), according to the first property of the characteristic functions (13.7.8), we obtain
 , (13.8.12)
, (13.8.12)
Where  - characteristic function of a random variable
- characteristic function of a random variable 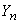 .
.
From formulas (13.8.12) and (13.8.3) we get
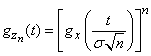 (13.8.13)
(13.8.13)
or using the formula (13.8.10),
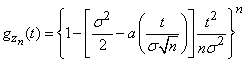 . (13.8.14)
. (13.8.14)
Let us name the expression (13.8.14):

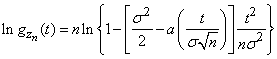 .
.
We introduce the notation
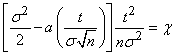 . (13.8.15)
. (13.8.15)
Then
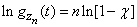 . (13.8.16)
. (13.8.16)
We will increase without limit 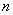 . The value of
. The value of 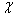 , according to the formula (13.8.15), tends to zero. With significant
, according to the formula (13.8.15), tends to zero. With significant 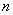 it can be considered very small. Decompose
it can be considered very small. Decompose  in a row and confine ourselves to one member of the expansion (the rest
in a row and confine ourselves to one member of the expansion (the rest  become negligible):
become negligible):
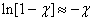 .
.
Then we get
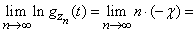
 .
.
By definition, the function 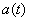 tends to zero at
tends to zero at 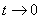 ; Consequently,
; Consequently,

and
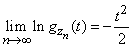 ,
,
from where
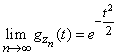 . (13.8.17)
. (13.8.17)
This is nothing but the characteristic function of a normal law with parameters 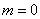 ,
, 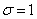 (see example 2,
(see example 2,  13.7).
13.7).
Thus, it is proved that by increasing 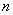 random characteristic function
random characteristic function 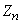 unboundedly approaches the characteristic function of the normal law; hence we conclude that the law of distribution of magnitude
unboundedly approaches the characteristic function of the normal law; hence we conclude that the law of distribution of magnitude 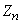 (and therefore the values
(and therefore the values 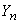 a) unlimited approach to normal law. The theorem is proved.
a) unlimited approach to normal law. The theorem is proved.
We have proved the central limit theorem for a particular, but important case of equally distributed terms. However, in a fairly wide class of conditions, it is also valid for unequally distributed terms. For example, A. M. Lyapunov proved the central limit theorem for the following conditions:
 , (13.8.18)
, (13.8.18)
Where 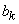 - the third absolute central moment of magnitude
- the third absolute central moment of magnitude 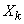 :
:

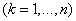 .
.
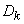 - variance of magnitude
- variance of magnitude 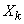 .
.
The most general (necessary and sufficient) condition for the validity of the central limit theorem is the Lindeberg condition: for any 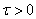
 ,
,
Where 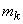 - expected value,
- expected value, 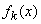 - distribution density of a random variable
- distribution density of a random variable 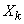 ,
, 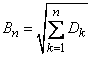 .
.
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis