13.3. The law of large numbers (Chebyshev theorem)

In this we prove one of the simplest, but at the same time the most important forms of the law of large numbers - the Chebyshev theorem. This theorem establishes a connection between the arithmetic mean of the observed values ​​of a random variable and its expectation.

First we solve the following auxiliary problem.

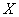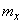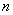There is a random variable with mathematical expectation and variance . Above this value is independent experiments and calculates the arithmetic average of all observed values ​​of 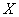. It is required to find the numerical characteristics of this arithmetic average - the expectation and variance - and find out how they change with increasing .

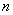Denote:

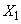- value 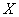in the first experience;

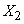- value 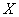in the second experiment, etc.

Obviously, a set of values 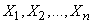represents 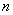independent random variables, each of which is distributed according to the same law as the quantity itself 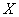. Consider the arithmetic average of these values:

.

Random value 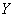there is a linear function of independent random variables 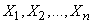. Find the expectation and variance of this value. According to the rules 10 to determine the numerical characteristics of linear functions, we obtain:

;

.

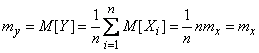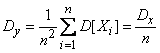So, the expected value of 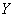does not depend on the number of experiences and equal to the expected value of the observed value 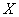; as for the variance of magnitude 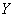then it decreases unlimitedly with an increase in the number of experiments and with a sufficiently large 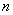can be made arbitrarily small. We see that the arithmetic mean is a random variable with an arbitrarily small variance and, with a large number of experiments, behaves almost as not random.

Chebyshev's theorem establishes in exact quantitative form this property of stability of the arithmetic mean. It is formulated as follows:

With a sufficiently large number of independent experiments, the arithmetic mean of the observed values ​​of a random variable converges in probability to its expected value.

We write the Chebyshev theorem as a formula. For this we recall the meaning of the term "converges in probability." It is said that a random variable 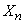converges in probability to value 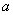if increasing 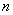probability that 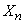and 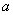will be arbitrarily close, unlimitedly approaching unity, which means that with a sufficiently large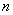

,

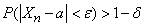Where 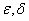- arbitrarily small positive numbers.

We write in a similar form the Chebyshev theorem. She claims that while increasing 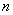average 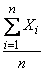converges in probability to 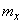i.e.

. (13.3.1)

Let us prove this inequality.

Evidence. Above it was shown that

has numeric characteristics

; .

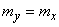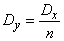Apply to random value 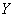Chebyshev's inequality, believing :

.

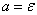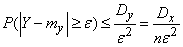No matter how small the number 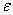you can take 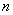so big that inequality holds

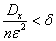
Where 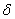- arbitrarily small number.

Then

,

whence, moving to the opposite event, we have:

,

Q.E.D.