9.4. The probability of hitting an ellipse

Among the few flat figures, the probability of hitting which can be calculated in the final form, belongs to the ellipse of dispersion (an ellipse of equal density).

Let the normal law on the plane be given in canonical form:

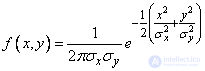. (9.4.1)

Consider the scattering ellipse whose equation

,

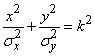where is the parameter 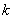is the ratio of the semiaxes of the dispersion ellipse to the main standard quadratic deviations. According to the general formula (8.3.3) we have:

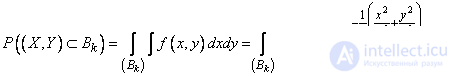. (9.4.2)

We make in the integral (9.4.2) the change of variables

.

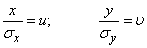This substitution ellipse converted to a circle 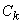radius 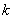. Consequently,

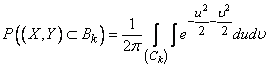. (9.4.3)

We proceed in the integral (9.4.3) from the Cartesian coordinate system to the polar one, setting

. (9.4.4)

The conversion Jacobian (9.4.4) is 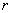. Making the change of variables, we get:

.

Thus, the probability of hitting a random point in the dispersion ellipse, whose semi-axes are equal 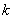standard deviations equal to:

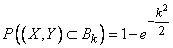. (9.4.5)

As an example, we find the probability of hitting a random point distributed according to the normal law on the plane in the unit ellipse of dispersion, whose semi-axes are equal to the mean square deviations:

.

For such an ellipse . We have:

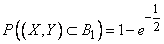
Using table 2 of the application, we find:

.

Formula (9.4.5) is most often used to calculate the probability of hitting a circle with circular scattering.

Example. On the path of a fast moving small size target 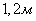put a fragmentation field in the form of a flat disk of radius . Inside the disk, the density of the fragments is constant and equal to 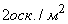. If the target is covered with a disk, then the number of fragments falling into it can be considered distributed according to the Poisson law. Due to the smallness of the target, it can be considered as a point and it can be considered that it is either completely covered by a fragmentation field (if its center falls within a fragmentation circle), or not at all covered (if its center does not fall within a circle). A hit of a shard guarantees defeat of the target. When aiming center circle 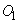seek to combine in the plane 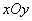with origin 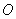(target center), but due to point errors 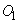scatters about 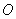(fig. 9.4.1). The law of dispersion is normal, the dispersion is circular, 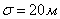. Determine the probability of hitting the target. .

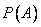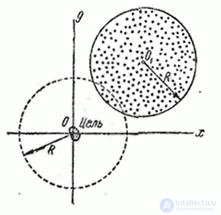
Fig. 9.4.1

Decision. For a target to be hit by shrapnel, it is necessary to combine two events: 1) hitting a target (point 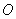) in a fragmentation field (circle of radius 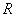) and 2) defeat the target, provided that the hit occurred.

The probability of hitting a target in a circle is obviously equal to the probability that the center of the circle (a random point 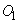) gets into a circle of radius 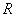, described around the origin. Apply the formula (9.4.5). We have:

.

The probability of hitting a target in a fragmentation field is:

.

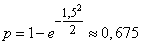Next, we find the probability of hitting the target. 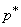provided it is covered with a fragmentation disk. Average number of shards 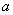that fall into a covered field target is equal to the product of the target area and the density of the fragment field:

.

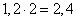Conditional probability of hitting the target 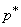there is nothing like the probability of hitting at least one fragment in it. Using the formula (5.9.5) of chapter 5, we have:

.

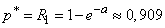The probability of hitting a target is:

.

Let us use the formula (9.4.5) for the probability of hitting the circle in order to derive one important distribution for practice: the so-called Rayleigh distribution.

Consider on the plane (fig. 9.4.2) random point scattering around the origin according to a circular normal law with a standard deviation . Find the distribution law of a random variable 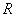- distance from point to the origin, i.e. lengths of a random vector with components .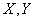

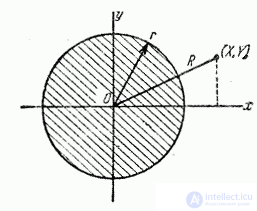
Fig. 9.4.2.

We first find the distribution function 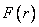magnitudes 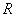. By definition

.

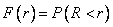This is nothing but the probability of hitting a random point. inside a circle of radius 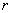(fig. 9.4.2). By the formula (9.4.5), this probability is equal to:

,

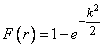Wher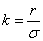e i.e.

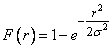. (9.4.6)

This expression of the distribution function makes sense only for positive values. 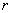; with negative 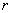need to put .

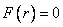Differentiating the distribution function 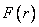by 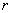let's find the distribution density

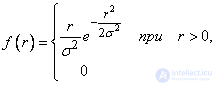(9.4.7)

The Rayleigh law (9.4.7) is found in different areas of practice in shooting, radio engineering, electrical engineering, etc.

Function graph 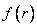(density Rayleigh law) is shown in Figure 9.4.3.

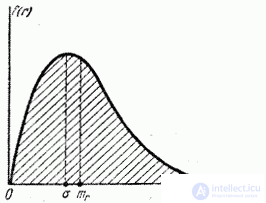
Fig. 9.4.3

Find the numerical characteristics of the value 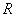distributed according to the Rayleigh law, namely: its fashion 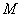and mathematical expectation 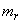. In order to find the mode — the abscissa of the point at which the probability density is maximum, we differentiate 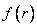and equate the derivative to zero:

.

The root of this equation is the desired mode.

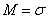. (9.4.8)

Thus, the most probable distance value 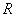random point from the origin is equal to the mean square deviation of dispersion.

Expected value 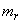find the formula

.

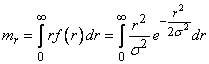Replacing a variable

.

we will receive:

.

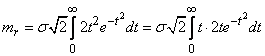Integrating in parts, we find the expectation of the distance :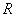

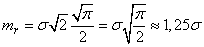. (9.4.9)