12.7. Linear functions of normally distributed arguments

Given a system of random variables 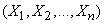subordinate to the normal distribution law (or, in short, “formally distributed”); random value 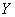is a linear function of these quantities:

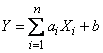. (12.7.1)

It is required to find the distribution law .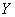

It is easy to verify that this is a normal law. Indeed, the magnitude 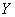is the sum of linear functions, each of which depends on one normally distributed argument 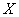, and it was proved above that such a linear function is also normally distributed. Adding several normally distributed random variables, we again obtain the value normally distributed.

It remains to find the parameters of 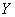- center of dispersion 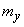and standard deviation 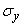. Applying the theorems on the expectation and variance of a linear function, we obtain:

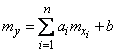, (12.7.2)

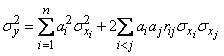, (12.7.3)

Where 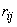- coefficient of correlation of quantities .

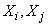In the case where the values 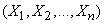uncorrelated (and therefore, under normal law, and independent), the formula (12.7.3) takes the form:

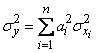. (12.7.4)

The standard deviations in formulas (12.7.3) and (12.7.4) can be replaced by proportional probable deviations.

In practice, it is often the case that the laws of the distribution of random variables 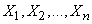included in the formula (12.7.1) are not exactly known, only their numerical characteristics are known: mathematical expectations and variances. If at the same time values 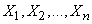independent and their number 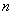is large enough, so, as a rule, it can be argued that, regardless of the form of the laws of distribution of quantities 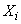, distribution law 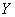close to normal. In practice, to obtain a distribution law, which can be approximately taken as normal, it is usually sufficient 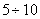terms in expression (12.7.1). It should be noted that this does not apply to the case when the dispersion of one of the terms in the formula (12.7.1) is overwhelmingly large compared to all the others; it is assumed that random terms in the sum (12.7.1) in their scattering have approximately the same order. If these conditions are met, then for 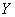a normal law can be approximately adopted with the parameters defined by formulas (12.7.2) and (12.7.4).

Obviously, all the above considerations about the distribution law of a linear function are valid (of course, the approximation is also for the case when the function is not exactly linear, but can be linearized).