16.2. Canonical decomposition of a random function

Consider a random function 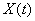given by decomposition

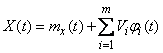, (16.2.1)

where are the coefficients 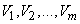represent a system of random variables with a mathematical expectation equal to zero and with a correlation matrix .

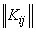Find the correlation function and the variance of the random function. .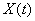

By definition

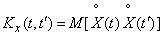, (16.2.2)

Where

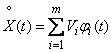, (16.2.3)

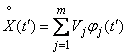. (16.2.4)

In the formula (16.2.4) the summation index is designated by the letter 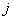to emphasize its independence from the summation index 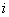in the formula (16.2.3).

Multiplying expressions (16.2.3) and (16.2.4) and applying to the product the operation of expectation, we get:

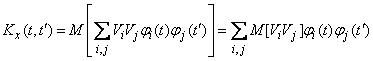, (16.2.5)

where summation applies to all pairs of values 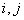- both equal and unequal. In the case when ,

,

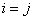Where 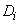- variance of random variable 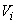. In the case when ,

,

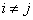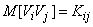Where 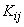- correlation moment of random variables .

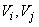Substituting these values ​​into formula (16.2.5), we obtain the expression for the correlation function of the random function 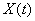given by the decomposition (16.2.1):

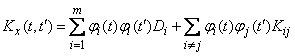. (16.2.6)

Assuming in expression (16.2.6) 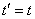get the variance of the random function :

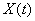. (16.2.7)

Obviously, expressions (16.2.6) and (16.2.7) take an especially simple form, when all coefficients 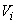decompositions (16.2.1) are uncorrelated, i.e. 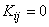at 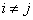. In this case, the decomposition of a random function is called "canonical."

Thus, the canonical decomposition of a random function 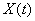its representation is called as:

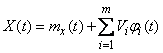, (16.2.8)

Where 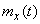- the expectation of a random function; 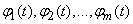- coordinate functions, and 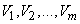- uncorrelated random variables with mathematical expectations equal to zero.

If the canonical decomposition of a random function is given, then its correlation function 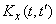expressed quite simply. Assuming in the formula (16.2.6) 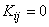at 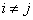, we get:

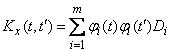. (16.2.9)

The expression (16.2.9) is called the canonical decomposition of the correlation function.

Assuming in the formula (16.2.9) 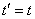get the variance of the random function

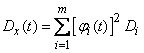(16.2.10).

Thus, knowing the canonical decomposition of a random function 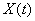, you can immediately find the canonical decomposition of its correlation function. It can be proved that the reverse situation is also true, namely: if the canonical decomposition of the correlation function (16.2.9) is given, then for a random function 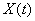fair canonical decomposition of the form (16.2.8) with coordinate functions and coefficients 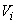with dispersions 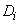. We will accept this provision without special proof.

The number of members of the canonical decomposition of a random function can be not only finite, but also infinite. We will meet examples of canonical expansions with an infinite number of members in Chapter 17. In addition, in some cases, so-called integral canonical representations of random functions are used, in which the sum is replaced by an integral.

Canonical expansions are applied not only for real, but also for complex random functions. Consider a generalization of the concept of canonical expansion for the case of a complex random function.

An elementary complex random function is called a function of the form:

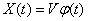, (16.2.11)

where as a random variable 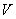so function 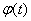are complex.

We define the correlation function of an elementary random function (16.2.11). Using the general definition of the correlation function of a complex random function, we have:

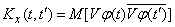, (16.2.12)

where the bar at the top, as before, denotes the complex conjugate value. Bearing in mind that

,

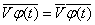and carrying out non-random values 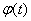and 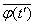for the sign of the mathematical expectation, we get:

.

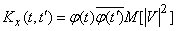But according to 15.9, 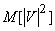is nothing but the variance of a complex random variable :

,

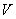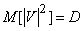Consequently,

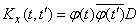. (16.2.13)

The canonical decomposition of a complex random function is its representation in the form:

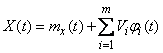, (16.2.14)

Where 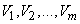- uncorrelated complex random variables with a mathematical expectation of zero, and 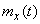, 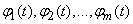- complex non-random functions.

If a complex random function is represented by a canonical expansion (16.2.14), then its correlation function is expressed by the formula

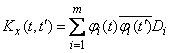, (16.2.15)

Where 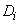- variance of magnitude :

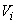. (16.2.16)

The formula (16.2.15) directly follows from the expression (16.2.13) for the correlation function of an elementary complex random function.

The expression (16.2.15) is called the canonical decomposition of the correlation function of a complex random function.

Putting in (16.2.15) 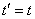, we obtain an expression for the variance of the complex random function given by the decomposition (16.2.14):

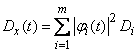. (16.2.17)