Lecture
There is a whole class of experiments for which it is easy to estimate the probabilities of their possible outcomes directly from the conditions of the experiment itself. For this, it is necessary that the various outcomes of the experiment have symmetry and, therefore, are objectively equally possible.
Consider, for example, the experience of throwing a die, i.e. symmetric cube, on the edges of which a different number of points is applied: from 1 to 6.
By virtue of the symmetry of the cube, there are grounds to consider all six possible outcomes of the experiment to be equally possible. That is what gives us the right to assume that with repeated throwing of a bone, all six faces will fall out about equally often. This assumption for a correctly performed bone is indeed justified by experience; With repeated throwing of a bone, each face of it appears approximately in one sixth of all cases of throwing, and the deviation of this fraction from 1/6 is the smaller, the greater the number of experiments made. Bearing in mind that the probability of a reliable event is taken equal to one, it is natural to attribute to the loss of each individual face a probability equal to 1/6. This number characterizes some objective properties of this random phenomenon, namely, the symmetry property of six possible outcomes of the experiment.
For any experience in which possible outcomes are symmetrical and equally possible, a similar technique can be used, which is called direct probability calculation.
The symmetry of possible outcomes of experience is usually observed only in artificially organized experiments, such as gambling. Since the initial development of the theory of probability was precisely on gambling schemes, the method of directly calculating probabilities, which historically arose along with the emergence of the mathematical theory of random phenomena, was long considered basic and was used as the basis of the so-called “classical” theory of probability. At the same time, experiments that did not have the symmetry of possible outcomes were artificially reduced to a “classical” scheme.
Despite the limited scope of practical applications of this scheme, it is nevertheless of a certain interest, since it is precisely on experiments with the symmetry of possible outcomes and on events related to such experiments that it is easiest to get acquainted with the basic properties of probabilities. This kind of events that allow direct calculation of probabilities, we will deal first.
We first introduce some auxiliary concepts.
1. Full group of events.
It is said that several events in a given experiment form a complete group of events if, as a result of the experiment, at least one of them must appear.
Examples of events that make up the full group:
1) the loss of the coat of arms and the loss of numbers when throwing a coin;
2) hit and miss when fired;
3) the appearance of 1,2,3,4,5,6 points when throwing a dice;
4) the appearance of a white ball and the appearance of a black ball when removing one ball from an urn, in which there are 2 white and 3 black balls;
5) not a single typo, one, two, three or more than three typos when checking the page of the printed text;
6) at least one hit and at least one miss with two shots.
2. Incompatible events.
Several events are called incompatible in this experience, if no two of them can appear together.
Examples of incompatible events:
1) the loss of the coat of arms and the loss of numbers when throwing a coin;
2) hit and miss when fired;
3) the appearance of 1.3, 4 points with one throwing a dice;
4) exactly one failure, exactly two failures, exactly three failures of the technical device for ten hours of operation.
3. Equal events.
Several events in this experience are called equally possible, if according to the conditions of symmetry there is reason to believe that none of these events is objectively more possible than the other.
Examples of equally possible events:
1) the loss of the coat of arms and the loss of numbers when throwing a coin;
2) the appearance of 1.3, 4, 5 points when throwing a dice;
3) the appearance of a card of diamonds, of hearts and clubs, when drawing a card from a deck;
4) the appearance of a ball with # 1, 2, 3 when removing one ball from an urn containing 10 numbered balls.
There are groups of events that have all three properties: they form a complete group, incompatible and equally possible; For example: the appearance of the coat of arms and numbers when throwing a coin; the appearance of 1, 2, 3, 4, 5, 6 points when throwing a dice. Events that make up such a group are called cases (aka “chances”).
If any experiment in its structure has the symmetry of possible outcomes, then the cases are an exhaustive system of equally possible and mutually exclusive outcomes of experience. This experience is said to be “reduced to a pattern of cases” (otherwise, to an “urn pattern”).
The pattern of cases takes place predominantly in artificially organized experiments in which the same possibility of experience outcomes (as, for example, in gambling) is deliberately and consciously ensured. For such experiments, a direct calculation of probabilities is possible, based on an estimate of the proportion of so-called "favorable" cases in the total number of cases.
An event is said to be favorable (or “favoring”) to some event if the occurrence of this event entails the occurrence of the given event.
For example, when throwing a die, six cases are possible: the appearance of 1, 2, 3, 4, 5, 6 points. Of which event 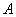 - the appearance of an even number of points - three cases are favorable: 2, 4, 6 and the other three are not favorable.
- the appearance of an even number of points - three cases are favorable: 2, 4, 6 and the other three are not favorable.
If experience is reduced to a pattern of cases, then the probability of an event 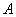 in this experience can be estimated by the relative proportion of favorable cases. Event probability
in this experience can be estimated by the relative proportion of favorable cases. Event probability 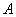 calculated as the ratio of the number of favorable cases to the total number of cases:
calculated as the ratio of the number of favorable cases to the total number of cases:
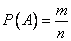 , (2.2.1)
, (2.2.1)
where P (A) - the probability of the event 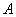 ;
; 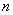 - total number of cases;
- total number of cases; 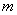 - the number of cases favorable event
- the number of cases favorable event 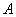 .
.
Since the number of favorable cases is always between 0 and 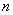 (0 - for the impossible and
(0 - for the impossible and 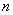 - for a reliable event), then the probability of an event calculated by the formula (2.2.1) is always a rational correct fraction:
- for a reliable event), then the probability of an event calculated by the formula (2.2.1) is always a rational correct fraction:
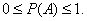 (2.2.2)
(2.2.2)
The formula (2.2.1), the so-called “classical formula” for calculating probabilities, has long been featured in the literature as the definition of probability. At present, when determining (explaining) probabilities usually proceed from other principles, directly associating the notion of probability with the empirical concept of frequency; the formula (2.2.1) is preserved only as a formula for the direct calculation of probabilities, suitable if and only when experience reduces to a scheme of cases, i.e. has a symmetry of possible outcomes.
Example 1. In the urn there are 2 white and 3 black balls. One ball is taken out of the urn at random. It is required to find the probability that this ball will be white.
Decision. Denote 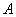 an event consisting in the appearance of a white ball. Total number of cases
an event consisting in the appearance of a white ball. Total number of cases 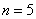 ; the number of cases favorable event
; the number of cases favorable event 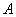 ,
, 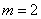 . Consequently,
. Consequently,
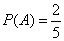 .
.
Example 2. In the urn a white and b black balls. From the urn removed two balls. Find the probability that both balls will be white.
Decision. Denote 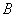 an event consisting in the appearance of two white balls. Calculate the total number of possible cases.
an event consisting in the appearance of two white balls. Calculate the total number of possible cases. 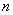 and the number of cases
and the number of cases 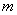 favorable event
favorable event 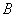 :
:
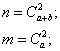
Consequently,

Example 3. In a batch of 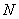 products
products 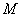 defective. From the party is chosen at random
defective. From the party is chosen at random 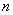 products. Determine the probability that among these n products will be exactly
products. Determine the probability that among these n products will be exactly 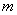 defective.
defective.
Decision. The total number of cases is obviously equal to 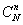 , number of favorable cases
, number of favorable cases 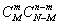 , whence the probability of the event that interests us
, whence the probability of the event that interests us
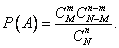
Comments
To leave a comment
Probability theory. Mathematical Statistics and Stochastic Analysis
Terms: Probability theory. Mathematical Statistics and Stochastic Analysis