Perhaps the most famous of them can be considered cellular automata under
name of the game "Life." Created the game "Life" was in 1970 by John Horton
Conway, a mathematician at the University of Cambridge. Arising in the game
situations are very similar to real processes occurring during the birth,
development and death of a colony of living organisms. For this reason, "Life" can
categories of games that imitate processes that are rapidly developing these days,
occurring in wildlife.
An infinite flat lattice of square cells is considered. Time
in this game is discrete (t = 0, 1, 2, ...). The cell can be alive or dead.
The change in its state at the next time t + 1 is determined by the state
its neighbors at time t (there are eight neighbors in a cell; four of them have common
edges, and four only vertices). The basic idea is to start with
some arrangement of cells, to follow the evolution of the initial position under
the action of Conway’s “genetic laws” that govern the birth, death
and cell survival. Conway carefully chose his rules and checked them for a long time.
in "practice", ensuring that they meet as many as possible three conditions:
• There should not be any initial configuration for which there would be
simple proof of the possibility of unlimited population growth.
• At the same time, there should be such initial configurations that
obviously have the ability to grow indefinitely.
• There should be simple initial configurations that during
considerable period of time grow, undergo various changes and
complete their evolution in one of the following three ways: completely
disappear (either due to overcrowding, i.e. too high density
living cells, or vice versa, due to the sparsity of the cells that form
configuration); go into a stable configuration and stop changing
in general, or, finally, go to the oscillatory mode, that is, the infinite
cycle of transformations with a certain period.
The consequence of these requirements were the following rules of the game "Life":
1. Survival. Each cell that has two or three adjacent living cells,
survives and passes on to the next generation.
2. Doom. Every cell with more than three neighbors dies due to
overcrowding. Every cell around which all neighboring cells are free
or only one cell is occupied, dies from loneliness.
3. Birth. If the number of occupied cells, which is bordered by some empty
the cell is exactly three, then on this cell the birth of a new
organism.
Let us ask ourselves the questions: What are the main types of structures (i.e. configurations,
defining the behavior of communities at large times) may exist in
such a system? What are the laws of organization of structures here? Can they
to interact, and what does this lead to? Find out what patterns are
the consequences of the above rules.
The first regularity - localization property - structures separated
two “dead” (empty) cells do not affect each other.
The second pattern is the cell system, which is described by the game "Life",
develops irreversibly. In fact, the configuration at time t is completely
determines the future (state at times t + 1, t + 2, and so on). But recover
the past of the system in its present fails. The picture here is the same as in
one-dimensional mappings, only preimages of this configuration can be
infinitely many. (Let us prove this statement: use the localization property
and put around this configuration a lot of localized single
cells or their pairs so that they do not affect it and each other. It is clear that all
they will disappear in the next step, in no way affecting the future of the system).
Here we can notice the signs of nonlinear dissipative structures: these
structures determined the behavior of the system when t tends to infinity in
case of different initial data.
The third pattern - as shown by long-term observations of
the process of the development of colonies, configurations that did not have at the beginning of the game
symmetry, tend to transition to symmetric forms.
The acquired symmetry properties in the process of further evolution are not lost,
configuration symmetry can only be enriched.
We agree to classify cell configurations by the following
parameters:
• By the number of cells in the combination: single cell, doublet (2 cells per
combinations), triplet (3 cells), etc.
• By developmental perspective: developing (unlimited growth), stable
(the number of cells in a population fluctuates around some mean),
endangered (the population is steadily decreasing), periodic (number
cell takes several fixed values through a certain
period).
Now consider the typical structures that appear in the game "Life".
The simplest are stationary, that is, time-independent structures.
(Conway himself calls them "lovers of a quiet life"). Their examples are shown in
Figure 1. With these stationary structures you can get a lot
others. In fact, if we have such a structure, then the configuration obtained
turning 90 o
will also be stationary. Bottom row configurations
show how you can complete construction of certain structures to any size.
Using the property of localization, one can build “large” stationary structures.
from "small" -elementary.

Fig.1. Examples of stationary structures implemented in the game "Life"
We can assume that stationary structures repeat themselves at each step.
on time. But there are other configurations that repeat themselves in N steps, so
called N-cycles (periodic structures).
Examples of 2-cycles are shown in Figure 2. With the evolution of various
Communities often encounter a 2-cycle, shown in the second line and called
"Semaphore"
Many different periodic configurations are known. but
efficient algorithms that allow building various configurations with a given
period N, apparently, is not currently created.
The evolution of randomly taken initial data often leads to
the simplest localized structures (shown in Figure 1) and semaphores.
However, more complex types of evolution are possible, for example, when the community
cells are symmetrically “completed”, and there are cycles of a long period,
having a complex shape.
In the game "Life" there are configurations that can move along
plane. One of them is a "glider" (or "glider") - a configuration of 5
cells (Fig. 3)
After the second turn, the glider shifts a little and is reflected relative to the diagonal.
As a result of two subsequent moves, the glider “comes out of the peak”, falls on
the previous course and moves one cell to the right and one cell down relative to
starting position.
The speed with which the chess king moves on the board in any
direction, Conway calls the "speed of light." Conway's choice fell on this
the term is due to the fact that in the game he invented great speeds simply do not
are achieved. No configuration reproduces itself fast enough
to move so fast. Conway has proven that maximum speed on
diagonal is one quarter of the speed of light. As the glider goes by itself
in itself after four moves and at the same time descends one cell diagonally,
it is said to slide across the field at a speed equal to one-fourth the speed
Sveta. Conway also showed that the speed of any final figure,
moving vertically or horizontally on free cells cannot
exceed half the speed of light. (The speed of movement is equal to the fraction in the numerator
which is the number of moves needed to reproduce the figure, and in
the denominator is the number of cells by which it shifts during this). It is clear that by virtue
symmetries there are gliders extending along any diagonal of a square in
both directions.
However, some configurations can move not along the diagonals, but
on vertical and horizontal straight lines. These are, for example, three "ship"
shown in Figure 4. (Note that not all
This type of configuration will be a ship). By the way, the glider is a ship
lightest weight. During the movement of the ships there are "spark", which immediately
go out with the further movement of ships.

Fig. 2. Examples of periodic structures (2-cycles) implemented in the game "Life" (toad, semaphore, clock)
Figure 3. Glider - gliding configuration of 5 cells
Single ships without an escort cannot occupy more than six cells in length,
Otherwise, various small pieces begin to appear on the field.
obstructing the movement of the ship. Conway found that longer
ships (which he called “super heavy”) need an escort of two or
a larger number of smaller ships. Escort ships do not give rise
obstacles in the way of a super heavy ship. Conway calculated that the ship is long
in one hundred cells requires an escort consisting of thirty-three (!) ships.
So, we have gliders and various ships. The question arises,
what happens when they collide with each other or with different
stationary configurations (hospitals). Collisions can be very
varied depending on the course of the airframe and its phase in the collision.
A collision between two gliders or a glider with a hospital can result in them
"Annihilation." A collision can produce a whole set of semaphores and
hospitals.
Pay attention to the following pattern. If the configuration is all
time is localized in a square of size NxN, then it is a set of hospitals and
cycles whose period does not exceed 2 ^ N
. In fact, each cell can
to be in one of two states, and all cells in the N ^ 2 region; therefore, when t> 2 ^ N
configurations will begin to repeat.
Fig. 4. Ships - configurations implemented in the game "Life", able to move
Considering continuous media, we can talk about resonant
excitement - initial data leading to a more complex evolution of solutions,
than in other cases. In the game "Life" there is an analogue of this behavior. Let's turn
attention to the configuration shown in Figure 5, called “r-pentemino”.
The arising cells occupy an increasing part of the plane, several
gliders, and this community will develop further. None of the other five-cell configurations result in such complex behavior.

Fig. 5. 5 cell configuration
showing the resonance effect
excitement (r-pentemino).
Fig. 6. Glider (catapult) -
configuration that generates
every 30 moves a glider.
As a rule, the evolution of the configurations taken at random leads to the appearance
sets of hospitals, semaphores, gliders. The total number of cells at t,
tending to infinity turns out to be limited (it was laid in
requirements of Conway), however, with some initial data, the evolution of the system
can qualitatively change. This behavior is characteristic of a number of biological
systems, in particular, evolutionary processes. An unlikely event may
qualitatively change the behavior of the system, lead to the emergence of new species.
That is why the game "Life" is used in environmental models, with
modeling of morphogenesis, in other biological problems.
The larger the community area, the more difficult it can be.
to lead. Therefore, unlimitedly growing in space
configurations. One of them, called the "catapult" or "glider gun",
He proposed in 1970 R. Gosper Jr. It can be seen that the catapult every 30
steps repeats itself and releases the glider (see Figure 6). Glider gun
fills the space with a stream of gliders. Conway hypothesized, according to
which there is no initial configuration capable of infinitely
grow. In other words, any configuration consisting of a finite number of living
cells can not go into a configuration in which the number of living cells
would exceed a certain final limit. But the hypothesis was wrong!
The refutation is a glider gun.
There are even more complex communities of cells that can move, leaving
for a large set of semaphores and hospitals. One of them is the “steam train” (he
has a rather complicated structure). Search for such configurations is pretty
time-consuming process, requiring the use of special algorithms and the power
qualified professionals.
Special configurations were also found, which John Tukey called
"Gardens of Eden." The Gardens of Eden cannot arise during the work of the cellular
automaton, since no configuration can generate them. Because of this
they must be set from the very beginning - in the zero generation. Not having
predecessors, they cannot be self-replicating. Alwi R. Smith
Found a way to apply Moore's theorem to Conway's game and showed that the configuration
the type of "Garden of Eden" is possible in the "Life". Formulas derived by moore
allowed Smith to argue that such a configuration could always be
enclosed in a square with a side of 10 000 000 000 cells.
The given examples show that in the discussed discrete system
There are a large number of different types of ordering that
determine the asymptotic behavior of a certain set of configurations (in this
sense, they turn out to be equivalent to attractors of dynamical systems). but
you can prove more - in the game "Life" there are arbitrarily complex types
ordering, this discrete system turns out to be equivalent to universal
computer machine.
A computer can be considered as a finite set of the simplest logical
elements performing operations AND, OR, NOT in a certain way
connected by wires, through which a set of pulses propagates,
coding sequence of zeros and ones. As a generator of such
impulses in the game "Life" stands a glider gun. The presence of a glider in the stream
it is natural to interpret as a unit, the absence as a zero. Clash
gliders, leading to their annihilation, allows you to build an element NOT by sending
two streams at right angles (if there is a glider in a certain place in the first
after the collision the glider in another stream on this place will disappear). More
other elements are constructed in a complex way.
For the analysis of situations arising in the game "Life", a computer is used.
The program simulating this cellular automaton uses a square
matrix, which is the field for the game. When changing the course, each is analyzed.
element of the old matrix and is based on its new, which corresponds to
configurations in the next step of evolution. For more detailed research
Conway game expanded to several populations, each of which develops
to your rules. The rules for each population are selected from the following:
• Conditions of birth and death. Four parameters are set (parameters can be
change during the game): minimum and maximum number of neighbors
the population at which a cell is born; minimum and maximum
the number of neighbors at which the cell survives and passes into the next
generation.
• Neighboring cells can be any cells that are in a 3x3 square with
center in this cell.
The game "Life" has found its use in biology as the game "Aqua-Tor",
which models the behavior of a system consisting of two populations, conditionally
called "herbivores" and "predators."
Tasks Game "Life"
1) Standard Rules
• Explore the rules of evolution in the game. Consider the dynamics of the simplest
populations: one cell, two cells, different configurations of three and
four cells. Find five triplets (configurations consisting of three
cells) that do not die in the next step of evolution.
• Consider the dynamics of all the above configurations.
• Consider the dynamics of the configurations in fig. 16, determine the nature of their
behavior. In the case of periodic dynamics find the oscillation period.
• Find your own initial configurations in the game "Life", which
meet the following requirements:
a) over time, the population "dies."
b) with the passage of time in the system is observed the formation of a stationary
states
c) after the transition process in the system there are periodic
fluctuations with a period of 2.
d) after the transition process, periodic
fluctuations with a period of 3.
e) after the transition process, periodic
fluctuations with a period of 4.
e) the population for a sufficiently large time (more than 70 steps) does not come to
any regular behavior or steady state.
• Investigate the dynamics of the configuration called Glider Gun. (Fig.
6)
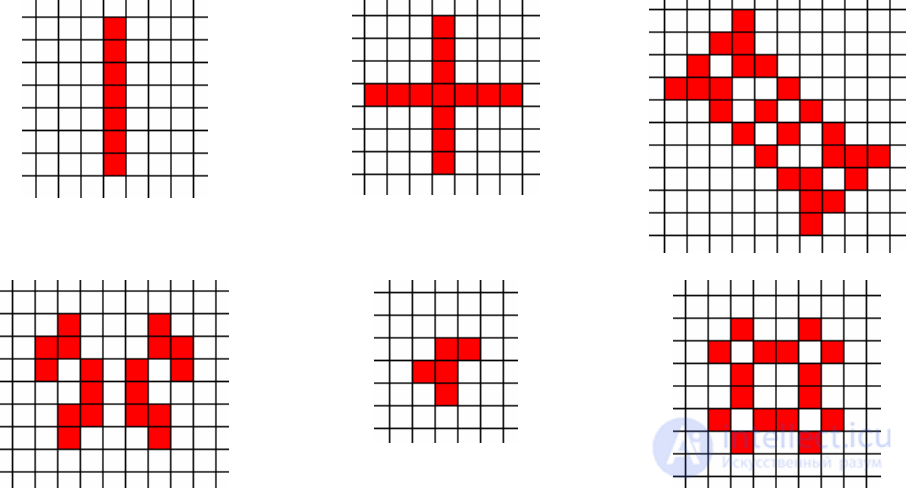

Fig. sixteen
2) Modified rules
• Place two populations on the plane, each in the “r-
pentamino ”(Fig. 16e). According to the statistics graph, wait until both come to the
stationary level (straight lines on the chart after 2100 steps). Explain why
initially identical configurations have different stationary levels.
• Investigate the collision of two gliders of different colors. What is the difference from
case of one population?
• Place a blue “block” on the field. Change the properties of the blue population
as follows: remove one corner cell from the neighborhood of the cell and
set model 2323. Follow a few steps of configuration evolution.
Explain the result. Estimate the speed of movement received
front.
• With these parameters, place a blue block and a red block with
standard parameters (model 3323, a neighborhood of 8 cells). To explore
interaction of populations, explain why blue dominates.
• achieve the parameters under which a single cell on the field survives and in
its development moves up the field.
• Place two squares on the field in the same neighborhood. Achieve parameters when
which the resulting segment increases in length with each step.






Comments
To leave a comment
System modeling
Terms: System modeling