Lecture
Telegraph equations, like all other equations describing electrical phenomena, can be reduced to the particular case of Maxwell's equations. From the point of view of practice, it is assumed that the conductors consist of an endless chain of quadrupoles, each of which represents an infinitely short section of the line:
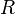 represented as a resistor (expressed in ohms per unit length).
represented as a resistor (expressed in ohms per unit length).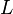 (arises due to the magnetic field around conductors, self-inductance, etc.) presented in the form of a coil (henry per unit length).
(arises due to the magnetic field around conductors, self-inductance, etc.) presented in the form of a coil (henry per unit length).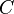 between two conductors is represented as a capacitor (farad per unit length).
between two conductors is represented as a capacitor (farad per unit length).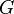 represented as a resistor between a live wire and a neutral wire (Siemens per unit length). In the model, this resistor has a resistance
represented as a resistor between a live wire and a neutral wire (Siemens per unit length). In the model, this resistor has a resistance 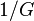 Ohm
OhmFor clarity, we repeat that the model is based on an endless chain of elements shown in the picture, and the denominations of its parts are indicated per unit length . You can also use  ,
, 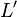 ,
, 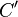 and
and 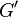 to emphasize that the values are derived by coordinate.
to emphasize that the values are derived by coordinate.
Consider the equivalent circuit of the transmission line presented in Fig. 1.8.
l
_img_14.jpg)
The voltage distribution in the cross sections of the line and the current along the conductors is determined generally by the basis of the system of equations: u (x) U H ch (x) I H sh (x);
UN (1.1)
i (x) I H ch (x) sh (x),
where U IZ is the boundary condition.
H NN
Consider a two-wire lossless line. In this case, the linear parameters R 1 0 and G 1 0, then the propagation coefficient and the characteristic impedance are determined by the expressions:
j
_img_15.jpg)
2 _img_16.jpg) L 1
L 1
0, k _img_17.jpg) L 1 C 1 ,
L 1 C 1 ,
.
L C 1
Then the system of equations (2.1) can be represented as: u (x) U cos (kx) j I sin (kx);
NN UN (1.2)
i (x) I cos cos (kx) js in (kx).
The value of the load resistance Z Н , while I Н 0 - idling. The amplitude distributions of voltage and current are shown in Fig. 1.9, a. The distribution of the phase voltage and current is shown in Fig. 1.9, b.
2
u m (x)
1.5
im (x)
one
0.5
0
_img_18.jpg) x
x
1 0.9 0.8 0.7 0.6 0.5 0.4 0.2 0.2 0.1 0 0
u (x) i (x)
but)
glad
_img_19.jpg) x
x
U (x)
_img_20.jpg)
_img_20.jpg)
_img_20.jpg)
_img_20.jpg) I (
I ( _img_21.jpg) x)
x)
_img_20.jpg)
b) Fig. 1.9 - Distribution of voltage and current along the transmission line The value of the load resistance Z N 0, while U N 0 is a short circuit. The amplitude distributions of voltage and current are shown in Fig. 1.10.
u m (x), im (x)
_img_22.jpg) x u (x) i (x)
x u (x) i (x)
_img_23.jpg)
Fig. 1.10 - Distribution of the normalized amplitude of voltage and current along the transmission line
The value of the load resistance Z N j X N , which is of a purely reactive nature. The distributions of the amplitude of voltage and current are presented in Fig. 1.11, when Z Н j.
u m (x)
im (x)
_img_24.jpg) x u (x) i (x)
x u (x) i (x)
Fig. 1.11 - The distribution of the normalized amplitude of voltage and current along the transmission line The value of the load resistance Z N Н R N , which has a purely active character. In this case, the normalized stress distribution is determined from (1.2) by the formula
2 2 2
um (x)
_img_25.jpg) cos (kx) sin (kx).
cos (kx) sin (kx).
R
H
The amplitude distributions of voltage and current are shown in Fig. 1.12 for the case when Z H 2.
_img_26.jpg)
along the transmission line
With a resistive load, Z Н , the maximum voltage amplitude is located at the load connection, the minimum is shifted by a distance equal to a quarter of the wavelength. At Z Н together the load connection is the minimum voltage, and the maximum is at a distance of a quarter of the wavelength from it.
The value of the load resistance Z Н R Н , equal to the wave resistance
eleven
transmission lines. The amplitude distributions of voltage and current are shown in Fig. 1.13. This mode of operation of the transmission line is called the traveling wave regime and is characterized by a constant value of the voltage and current amplitude along the transmission line. In this case, the phase of the current and voltage varies linearly.
the norm
1.5
im (x)
one
0.5
0
_img_27.jpg)
Comments
To leave a comment
Microwave Devices and Antennas
Terms: Microwave Devices and Antennas