Lecture
Основу математической модели многомерной системы во временной области составляет векторно-матричная форма записи системы дифференциальных уравнений первого порядка, которая носит название уравнения состояния. Уравнение состояния имеет вид –
|
|
(1) |
где 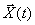 — вектор состояния размерности
— вектор состояния размерности 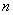 , который включает в себя переменные объекта, однозначно определяющие его состояние,
, который включает в себя переменные объекта, однозначно определяющие его состояние,

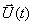 — вектор управления или входа размерности
— вектор управления или входа размерности 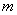 , который включает в себя сигналы, действующие на систему извне,
, который включает в себя сигналы, действующие на систему извне,

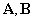 — матрицы параметров, включающие в себя параметры системы, размерность которых соответственно
— матрицы параметров, включающие в себя параметры системы, размерность которых соответственно  ,
,
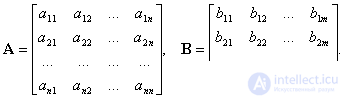
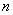 — порядок системы.
— порядок системы.
Иногда уравнение состояния (1) записывают в развернутой форме –
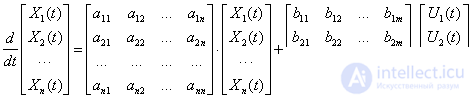 .
.
Уравнение состояния и структура полностью описывают объект управления, вектор состояния содержит переменные объекта, которые однозначно описывают его состояние.
Но в реальных системах многие компоненты не могут быть измерены или наблюдаемы с помощью датчиков. Эту ситуацию разрешает введение дополнительного уравнения выхода, которое определяет те переменные, которые доступны для наблюдения (на выходе системы) –
|
|
(2) |
где 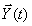 — вектор выхода размерности
— вектор выхода размерности 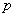 , который содержит переменные объекта, доступные для наблюдения,
, который содержит переменные объекта, доступные для наблюдения,

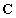 — матрица параметров размерности
— матрица параметров размерности 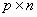 –
–

в системах управления 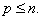
Уравнение выхода (2) также можно записать в развернутой форме

Графически уравнение состояния и уравнение выхода могут быть представлены в виде, показанном на рис. 1.

Рис. 1
Символ интегрирования на схеме означает покомпонентное интегрирование векторной величины.
В общем виде пространство состояний 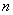 — мерной системы задается радиус-вектором
— мерной системы задается радиус-вектором 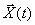 в координатной системе, оси которой определяются компонентами вектора состояния, как это показано на рис. 2.
в координатной системе, оси которой определяются компонентами вектора состояния, как это показано на рис. 2.

Рис. 2
Рассмотрим несколько примеров представления процессов в пространстве состояний.
Пример
Рассмотрим в пространстве состояний процесс пуска электродвигателя (М) постоянного тока с постоянными магнитами, принципиальная схема установки показана на рис. 3. Пуск производится подключением с помощью контакта (К) напряжения 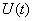 , при этом в цепи будет протекать ток
, при этом в цепи будет протекать ток 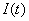 и двигатель будет вращать вал с нагрузкой (Н) со скоростью
и двигатель будет вращать вал с нагрузкой (Н) со скоростью 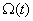 , ток и скорость определяются с помощью датчиков соответственно ДТ ДС.
, ток и скорость определяются с помощью датчиков соответственно ДТ ДС.
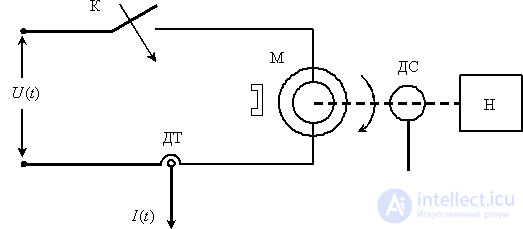
Рис. 3
Состояние двигателя в данном случае однозначно определяется током и скоростью двигателя, поэтому вектор состояния задаем в следующем виде –
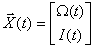 .
.
Вектор входа будет иметь только одну компоненту 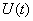 . Графики изменения во времени переменных двигателя показаны на рис. 4.
. Графики изменения во времени переменных двигателя показаны на рис. 4.
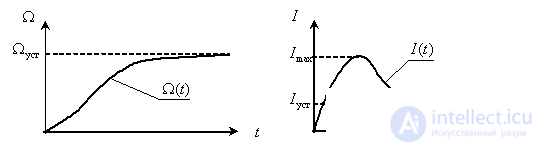
Рис. 4
На рис. 4 введены обозначения:  — установившиеся значения соответственно скорости и тока,
— установившиеся значения соответственно скорости и тока, 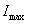 – максимальное значение тока при пуске.
– максимальное значение тока при пуске.
Сформируем двухмерное пространство состояний двигателя с траекторией движения конца вектора состояния в процессе пуска, для этого откладываем проекции вектора, то есть ток и скорость, в одинаковые моменты времени.

Рис. 5
Пример
Рассмотрим в пространстве состояний процесс позиционирования, то есть перемещения вала в заданное положение 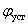 , в автоматизированном электроприводе, показанном на рис. 6.
, в автоматизированном электроприводе, показанном на рис. 6.
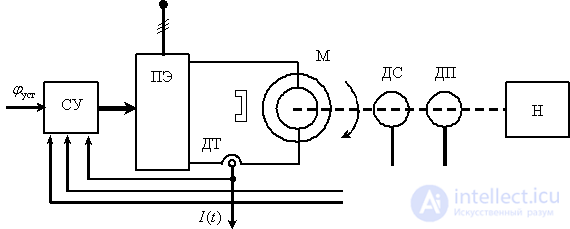
Рис. 6
В этом случае состояние двигателя и всей системы электропривода в целом определяют три переменные двигателя ток 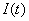 , скорость
, скорость 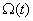 и положение вала
и положение вала 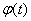 –
–
 .
.
Графики изменения во времени переменных двигателя показаны на рис. 7.
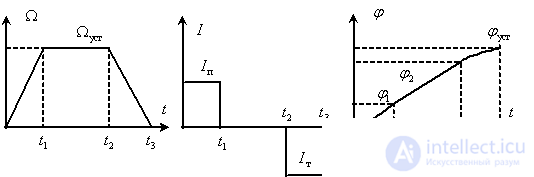
Рис. 7
Сформируем трехмерное пространство состояний электропривода с траекторией движения конца вектора состояния в процессе позиционирования по временным графикам изменения компонент вектора состояния.

Рис. 8
Теперь рассмотрим получения математической модели многомерного объекта в виде уравнений состояния на примере двухмассовой упругой механической системы, показанной на рис. 9.
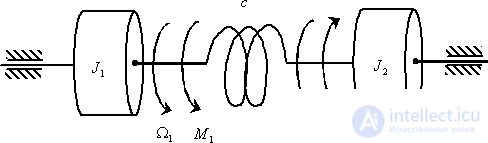
Рис. 9
Двухмассовая упругая система представляет собой механическую систему, состоящую из двух вращающихся масс с моментами инерции 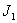 и
и 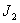 . К каждой массе прикладывается извне момент (
. К каждой массе прикладывается извне момент ( и
и 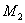 ), массы соединены валом, обладающим упругими свойствами (
), массы соединены валом, обладающим упругими свойствами (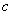 ), массы вращаются со скоростями
), массы вращаются со скоростями  и
и 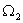 .
.
Система дифференциальных уравнений, описывающих систему, имеет вид –
|
|
(3) |
где 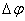 – разность углов положения первой
– разность углов положения первой 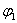 и второй
и второй 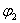 масс.
масс.
Так как уравнения состояния (1) и выхода (2) имеют единый для всех линейных систем вид, поэтому, чтобы определить их для конкретной системы мы должны выполнить следующее:
задать векторы состояния и входа, определив тем самым порядок системы и порядок вектора входа,
определить матрицы параметров уравнений.
Состояние системы определяется тремя переменными 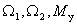 , поэтому задаем вектор состояния следующего вида –
, поэтому задаем вектор состояния следующего вида –
 .
.
Порядок системы 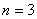 . Заметим, что положение переменных в векторе состояния можно задать произвольно, но в дальнейшем изменять его нельзя. Вектор входа определяется сигналами, действующими на систему извне, а это – моменты
. Заметим, что положение переменных в векторе состояния можно задать произвольно, но в дальнейшем изменять его нельзя. Вектор входа определяется сигналами, действующими на систему извне, а это – моменты 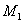 и
и 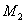 , поэтому вектор входа имеет вид –
, поэтому вектор входа имеет вид –
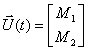 .
.
Порядок вектора выхода 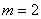 . Здесь также порядок следования компонент может быть произвольным, но фиксированным в дальнейших операциях.
. Здесь также порядок следования компонент может быть произвольным, но фиксированным в дальнейших операциях.
Преобразуем уравнения системы (3) к форме Коши –
|
|
(4) |
Нам требуется получить уравнение состояния для системы третьего порядка с вектором входа второго порядка, посмотрим, что представляет собой это уравнение в общем виде –
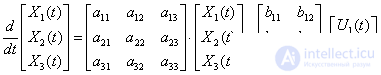 .
.
Раскрывая матричные скобки, получим –
|
|
(5) |
Теперь можно сформулировать задачу следующего этапа. Необходимо привести систему (4) в виду (5), для этого следует:
расположить уравнения в порядке следования компонент в векторе состояния,
расположить слагаемые в правых частях слева на право в порядке следования сначала компонент вектора состояния, затем вектора входа,
отсутствующие слагаемые заменяем произведениями переменных на нулевые коэффициенты.
В результате коэффициенты в правых частях при соответствующих компонентах векторов состояния и входа будут компонентами искомых матриц уравнения состояния.
Преобразуем систему (4) к виду (5), в результате получим –
|
|
(6) |
В результате по коэффициентам слагаемых в правых частях (6) получим искомые матрицы параметров уравнения состояния –

Уравнение состояния в развернутом виде –
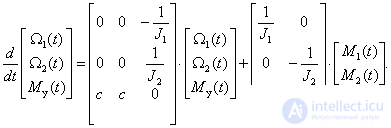
Вид уравнения выхода определяется тем, какие компоненты вектора состояния доступны для наблюдения. В электромеханических системах электроприводов, эквивалентом которых является упругая двухмассовая система, возможны три варианты датчиковых систем (полагаем датчики безынерционными, а коэффициенты преобразования датчиков единичными):
Датчики скорости установлены на обеих массах. Тогда имеем следующее уравнение выхода –
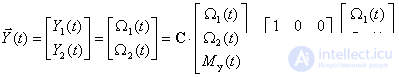
То есть имеем  ,
,

Датчик скорости установлен на первой массе, уравнение выхода –
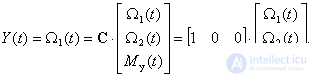
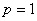 ,
, 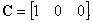
Датчик скорости установлен на второй массе, уравнение выхода –
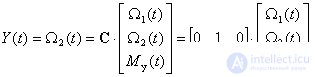
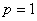 ,
, 
Контрольные вопросы и задачи
Перечислите компоненты уравнения состояния (векторы и матрицы), их размерности.
Поясните смысл уравнения выхода, перечислите компоненты и их размерности.
По системе дифференциальных уравнений, описывающих многомерную систему –
 ,
,
полагая векторы состояния и входа –
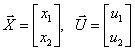 ,
,
записать уравнение состояния в развернутой форме.
Ответ:
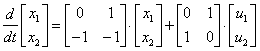 .
.
По уравнению состояния
 ,
,
описывающему многомерную систему, определить систему дифференциальных уравнений, связывающих компоненты векторов состояния и входа.
Ответ:
. .
.
По системе дифференциальных уравнений, описывающих многомерную систему –

полагая векторы состояния и входа –
 ,
,
записать уравнение состояния в развернутой форме.
Ответ:
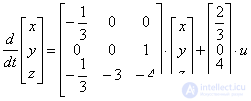
Comments
To leave a comment
Mathematical foundations of the theory of automatic control
Terms: Mathematical foundations of the theory of automatic control