Lecture
It is obvious that some images are more informative than others, i.e. they have more details or when analyzing they can extract more data. Details, data and other similar concepts are of high quality and rather vague. Therefore, it is often necessary to introduce quantitative characteristics of the image, allowing to evaluate the limiting properties of the algorithms for encoding, correcting and analyzing images. One of the approaches to the quantitative description of images is the application of information theory [39-42].
According to the method described in sect. 5.3, assume that the matrix 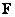 size
size 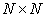 composed of quantized image samples will be replaced by a column vector.
composed of quantized image samples will be replaced by a column vector. 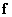 size
size 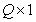 (Where
(Where 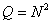 ), obtained by scanning the matrix
), obtained by scanning the matrix 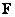 by columns. In principle, such vectors can be considered as images at the output of some source that can generate any of the possible vectors. In one of the extreme cases, a dark image is obtained with the minimum brightness of all elements, and in the opposite case, an image with maximum brightness. Between these extreme cases many different images are enclosed. If the brightness of each of
by columns. In principle, such vectors can be considered as images at the output of some source that can generate any of the possible vectors. In one of the extreme cases, a dark image is obtained with the minimum brightness of all elements, and in the opposite case, an image with maximum brightness. Between these extreme cases many different images are enclosed. If the brightness of each of 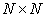 image elements are quantized to
image elements are quantized to  levels, this source can create
levels, this source can create  various images. Many of them have a chaotic structure and are similar to the realization of two-dimensional random noise. Only a very small number of
various images. Many of them have a chaotic structure and are similar to the realization of two-dimensional random noise. Only a very small number of 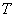 possible images will be what the real sensor would give when observing the world around us. In principle, we can assume that there is an a priori distribution
possible images will be what the real sensor would give when observing the world around us. In principle, we can assume that there is an a priori distribution 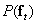 (Where
(Where 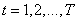 ) the probability of occurrence of each of the possible states of the vector
) the probability of occurrence of each of the possible states of the vector 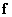 . To measure or model this distribution is very difficult, but the idea itself eventually leads to useful results.
. To measure or model this distribution is very difficult, but the idea itself eventually leads to useful results.
In 1948, Shannon [39] published his famous book The Mathematical Theory of Communication, in which he gave a method of quantitatively describing the properties of data sources and information transmission systems. The basis of the Shannon information theory is the concept of entropy. In the vector description of the image, the average amount of information in the image is equal to the source entropy:
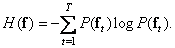 (7.6.1)
(7.6.1)
In this definition of entropy, logarithms with a base of two are used and entropy is measured in binary units. The source entropy is useful to know when encoding images, because according to the encoding theorem in the absence of interference [39], it is theoretically possible to encode images without an image distortion created by a source with entropy 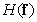 coding cost
coding cost 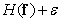 binary units where
binary units where 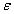 - infinitely small positive value. Conversely, in principle, it is impossible to encode images without distortion if the number of binary units is less than
- infinitely small positive value. Conversely, in principle, it is impossible to encode images without distortion if the number of binary units is less than 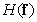 .
.
Probability of occurrence 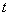 -th vector describing the image can be expressed in terms of the joint probability distribution of the brightness levels of the image elements
-th vector describing the image can be expressed in terms of the joint probability distribution of the brightness levels of the image elements
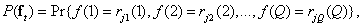 (7.6.2)
(7.6.2)
Where 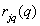 - meaning
- meaning 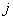 -th level of quantization for
-th level of quantization for 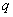 -go element. This probability can also be expressed as a product of conditional probabilities:
-go element. This probability can also be expressed as a product of conditional probabilities:
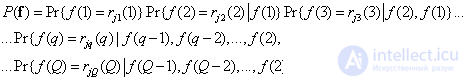 . (7.6.3)
. (7.6.3)
Logarithm both sides of equality (7.6.3) on the base two and taking into account the definition of entropy (7.6.1), we get
 . (7.6.4)
. (7.6.4)
In equality (7.6.4) 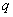 -e term, denoted by
-e term, denoted by  can be considered as an expression for the average information contained in
can be considered as an expression for the average information contained in 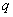 th component of the vector image
th component of the vector image 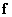 , provided that the brightness of the preceding
, provided that the brightness of the preceding 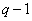 component. In this way,
component. In this way,
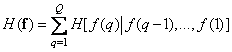 . (7.6.5)
. (7.6.5)
This expression, which describes the entropy of the source of images, is general and does not depend on the order in which the image elements are taken. Let us now consider the form of formula (7.6.5) for two cases: 1) the image is expanded in columns and 2) when all elements of the image arrive simultaneously. It can be shown that when you scan an image by columns
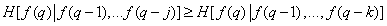 , (7.6.6)
, (7.6.6)
Where 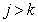 . This means that the information contained in
. This means that the information contained in 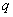 point, with an increase in the number of fully known preceding image elements only decreases on average. The equality of both parts of the relation (7.6.6) is achieved only when the brightness of all elements are distributed independently. If the number of known preceding elements increases indefinitely, then the right-hand side of inequality (7.6.6) tends to some non-zero limit value, denoted as
point, with an increase in the number of fully known preceding image elements only decreases on average. The equality of both parts of the relation (7.6.6) is achieved only when the brightness of all elements are distributed independently. If the number of known preceding elements increases indefinitely, then the right-hand side of inequality (7.6.6) tends to some non-zero limit value, denoted as 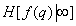 .
.
If we ignore marginal effects that are insignificant for fairly large images, then the image entropy can be approximately expressed as
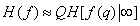 . (7.6.7)
. (7.6.7)
Thus, we can assume that the entropy of the entire image is equal to the limiting value of the conditional entropy of one image element multiplied by the total number of elements.
In systems with image scanning, the limiting conditional entropy is determined based on a finite sequence of previous elements. So, if these elements were 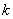 then
then
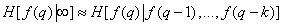 . (7.6.8)
. (7.6.8)
Explicitly
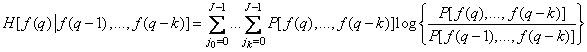 , (7.6.9)
, (7.6.9)
where is the joint probability distribution
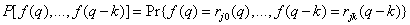 (7.6.10)
(7.6.10)
( 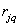 - levels of quantization of brightness). To calculate conditional entropy (7.6.9), it is necessary either to introduce a model of a joint probability distribution, or measure the corresponding frequency distributions for an image or a certain class of images.
- levels of quantization of brightness). To calculate conditional entropy (7.6.9), it is necessary either to introduce a model of a joint probability distribution, or measure the corresponding frequency distributions for an image or a certain class of images.
Table 7.6.1. Entropy Estimates for Images by Schreiber
|
Order |
Functional expression of entropy |
Entropy, bits / element |
|
The first |
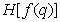 |
4.4 |
|
Second |
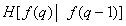 |
1.9 |
|
Third |
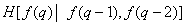 |
1.5
|
Schreiber [43] estimated the entropy of the first, second, and third order for several images quantized at 64 levels, measuring the distributions of relative frequencies of the same order. The resulting distributions were substituted into formula (7.6.10) instead of the corresponding probability distributions. With this method of measurement, it is assumed that the source of images is stationary and ergodic, that is, averaging over an ensemble of images can be replaced by averaging over a separate image. The results of measurements carried out by Schreiber for a particular image are shown in Table. 7.6.1. To encode this image using conventional PCM, six-bit code words are required, i.e. 6 bits / element are expended. Theoretically, 4.4 bits / element is sufficient for encoding, provided that all elements are encoded separately. If we use the value of the previous element, then the theoretical limit will be reduced to 1.9 bits / element. In other words, the previous element gives 2.5 bits of information about the element. 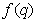 . Accounting for another preceding element gives only 0.4 bits of additional information. Thus, it turned out that in this image most of the additional information retrieved is contained in a small number of the previous elements.
. Accounting for another preceding element gives only 0.4 bits of additional information. Thus, it turned out that in this image most of the additional information retrieved is contained in a small number of the previous elements.
Above, a method for estimating the entropy of an image developed in columns, in which the limiting conditional entropy was described 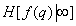 approximated by conditional entropy, calculated taking into account several previous elements in the same column. This method can be used to estimate the image entropy, when all its elements arrive simultaneously.
approximated by conditional entropy, calculated taking into account several previous elements in the same column. This method can be used to estimate the image entropy, when all its elements arrive simultaneously.
Assume that 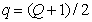 denotes the number of the central element of the vector
denotes the number of the central element of the vector 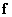 with an odd number of elements. Then the joint probability distribution can be represented as
with an odd number of elements. Then the joint probability distribution can be represented as
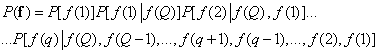 (7.6.11)
(7.6.11)
Repeating the reasoning that led to relation (7.6.7), the entropy of the source of images can be expressed by approximate equality
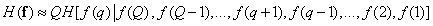 . (7.6.12)
. (7.6.12)
The obtained “two-sided” expression for conditional entropy can, in turn, be approximated, taking into account only the nearest elements of the column:
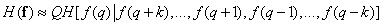 . (7.6.13)
. (7.6.13)
Developing this idea, one can include in the expression for the estimation of entropy all elements of the vector that have sufficiently strong statistical links with 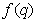 . In many cases, such elements are geometrically closest to the subject. Therefore, we can accept the following entropy estimate:
. In many cases, such elements are geometrically closest to the subject. Therefore, we can accept the following entropy estimate:
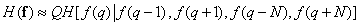 , (7.6.14)
, (7.6.14)
Where 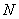 - the length of the column, and the entropy of the element
- the length of the column, and the entropy of the element 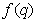 determined by the values of the next four elements, located above, below, to the right and to the left of it.
determined by the values of the next four elements, located above, below, to the right and to the left of it.
Preuss [44] calculated the entropy of two-grade facsimile documents using several preceding scan elements. Unfortunately, due to the excessive amount of computation required, it is difficult to estimate the entropy of multi-gradation images even using the simplified formula (7.6.14). For calculations using this formula, it is necessary to obtain a fifth order frequency distribution, and the number of possible values of each argument is equal to the number of luminance quantization levels. It is necessary to draw the sad conclusion that, in principle, the calculation of entropy makes it possible to estimate the “content” of the image, but for multi-gradation images such calculations are practically impossible.
Comments
To leave a comment
Digital image processing
Terms: Digital image processing