Lecture
In this section of the course, methods of representing numbers in a computer are considered, methods for performing arithmetic operations that are different from methods that are widely used in practice.
As you know, in the 19th century, the production of operations on numbers containing many digits was a difficult task that could only be solved by professionals. At this time, the basic rules for carrying out operations on multi-valued numbers by the Uzbek mathematician Al-Khorezmi were already developed. The general laws by which these rules were built, later received the name ALGORITHM. They are so widely entered into life that, making these operations on multi-valued numbers, we do not think about the fact that we follow a strict system of rules.
The method of representing an image of arbitrary numbers using some finite set of characters is called a number system.
In everyday practice, we use, as a rule, the decimal number system. The answer to the question: “Why is this system of accounts the most widespread?” - Now it is difficult to give. In the literature, as a rule, the justification is given to the fact that there are a total of 10 fingers on a person’s hands. It is unlikely that this justification can be taken seriously. In practice, we are faced with more complex, in particular, with mixed systems. For example, the system of counting time, where per unit is taken second, minute, hour, day, week, month, year. Or the system of counting money, until recently used in England (penny, shilling, pound):
12n = 1sh, 20sh = 1f.
Or even more interesting - the Roman counting system, which uses symbols: I - 1, V - 5, X - 10, L - 50, C - 100, D - 500, M - 1000.
This system is special and rarely used (dial, architecture, history, etc.)
Number systems can be divided into:
Let's start with the last. In these systems, each number is assigned its own symbol. These systems do not find wide application due to their natural limitations (alchemy, coded messages) —inumerable set of symbols, which is required to represent all possible numbers. Therefore, we omit these systems from consideration.
The very name of these systems indicates the relationship of the significance of the number and its image from the position.
Position is a place in which only one character can be represented.
An example of a positional number system is the decimal system.
In this system, the number is represented as a polynomial of the "n" degree, and is represented by a combination of some symbols, each of which has a different weight depending on the position it occupies.
a 4 a 3 a 2 a 1 is a number; a 1 , a 2 , a 3 , a 4 - characters.
All positions are assigned a different weight, which is most often chosen as the whole base degree of the system.
The base of the number system is a number, which is the power of many different characters allowed in each position of the number.
So for the decimal system are allowed characters: 0, 1, 2, 3, ..., 9.
Denote by "p" the base of the number system. Then the weights of the positions of the number can be represented as follows:
... p
3
p
2
p
one
p
0
.
The number itself, the image of which has the form, for example, a 3 a 2 a 1 a 0 can be represented as follows:
a 0 p 0 + a 1 p 1 + a 2 p 2 + a 3 p 3 is a detailed record of the number in the positional system.
For example:
973
ten
= 3 * 10
0
+ 7 * 10
one
+ 9 * 10
2
= 3 + 70 + 900.
Unlike the time counting system, the decimal system is homogeneous, i.e. the same decimal symbols are enough to represent any number. While in mixed systems, you need to invent all new and new characters in order to portray the next largest number.
Thus, homogeneity is one of the important properties of positional systems.
Any number X in the positional number system can be represented as:

Where
m is the number of positions or digits reserved for the image of the integer part of a number.
n is the total number of digits in the number.
a i is any valid character in the bit, i.e. a i = {0, 1, 2, ..., p-1}.
p - the base of the number system.
For example:
- 961.13 = - (9 * 10
2
+ 6 * 10
one
+ 1 * 10
0
+ 1 * 10
-one
+ 3 * 10
-2
).
pp
= 10p
... +3, +2, +1, 0, -1, -2, -3 ...
A natural question arises, is the generally accepted number system with base 10 optimal? If so, from what position? The question deserves attention, because one of the first VMs (ENIAC) used exactly the decimal system.
Direct and unequivocal answer to this question is impossible. Many different answers can be given, and all of them will be valid only for some specific conditions.
Introducing the general representation of a number in the positional system, we questioned the decimal values, not because it suddenly showed its negative qualities, but because its advantages are obvious only with manual counting methods. We are interested, first of all, of such a number system, which will be convenient and economical for automatic calculations using a computer. We must also remember that it is necessary for this to have a computer itself.
We show that the decimal system is not obsolete. For example, for the production of cost-effective calculations usually have to deal with very large volumes of numerical information. Then, with the introduction of the new system, I would have to use the following chain of actions:
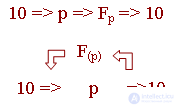
Those. it would be necessary to transfer information from the decimal system to the "p" system, perform the necessary operations on it in the "p" system, then do it again, but reverse the translation from the "p" system to the decimal one, since the rejection of the decimal system would require the elimination of the first stage.
If the conversion from the decimal system to the "p" system does not require too much time, at the same time, if the execution of the F function in the "p" system is done much faster, then this chain of actions will be justified.
But for economic information is characterized by the fact that very simple operations need to be performed every time over a large amount of source data. So in this case it is hardly advisable to move to a new system. This is the explanation of the fact that at present a significant number of computers are built precisely in the decimal number system.
However, computers are designed not only to perform economic calculations. In most cases, non-economic applications of computers deal with tasks in which the total amount of input data is small, but the total number of operations required is enormous. It is for these kinds of applications that the sequence of actions considered may prove beneficial.
It is obvious that it is possible, without limiting the scope of the computer, to be given the value of some of the largest numbers. Let it be a numberM. We use the positional number system with the base "p", and then we need the "n" digits to represent all the numbers:
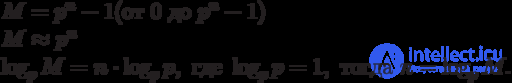
The equipment that is needed to store any number from 0 to M is proportional to the product of the base of the number system by the number of digits.
Thus, for a given number M, the number of digital-digits at the base of "p":
p * n = p * log
p
M, (6.1)
Where:
Digital Digit - Equivalent Equipment
p * n is the number of stable states of the memory element,
n is the number of digits in the number.
Consider an example :
Let there be 24 digital digits.
| Foundation p. | The possible number of digital digits. | The greatest number is M. |
| 2 | 2 * 12 |
1 * 1 * ... * 12 = 4095ten
\ ________ /
12
|
| 3 | 3 * 8 |
2 * 2 * ... * 23 = 6560ten
\ ________ /
eight
|
| four | 4 * 6 |
3 * 3 * ... * 3four = 4095ten
\ ________ /
6
|
| 6 | 6 * 4 |
5 * 5 * 5 * 56 = 1295ten
\ ______ /
four
|
| eight | 8 * 3 |
7 * 7 * 7eight = 511ten \ ____ / 3 |
The number of digital discharges speaks of the equipment size as well as a characteristic of speed. As we shall see later, in the positional number system, the execution times of operations can be expressed in terms of the number of digits in the number.
We consider "p" - the value of continuous. Find the derivative of (6.1) by the value of "p". We take the second derivative with respect to "p". We will see that the first derivative vanishes, and the second is greater than zero at p = e. Those. we get the minimum for p = e.
Thus, the system with base e is optimal in terms of equipment and speed.
But e = 2,718 ...
Therefore, the optimal is a system with base p = 3.
We construct a function that characterizes the ratio of equipment in the system with the base "p" relative to the system with the base "2".
| p | 2 | 3 | four | five | 6 | 7 | eight | 9 | ten |
| f (p) | 1,000 | 0.946 | 1,000 | 1,078 | 1,148 | 1,247 | 1,333 | 1,420 | 1,595 |
Those. The 10th system is more than 1.5 times uneconomical with respect to the 2nd system, and the 3rd system is only 5% more economical than the 2nd one.
The real rationale for the efficiency of a system looks somewhat more complicated.
When we talk about profitability, then, first of all, we mean the amount of equipment concentrated in the AU and memory. The amount of equipment of the CU is not so simple depending on the "p" and the AU takes into account only the equipment associated with the elements of information storage, but not the logical equipment.
A more detailed analysis shows that the most effective are systems with a multiple of 2, i.e. 2, 4, 8, 16. The specificity of the construction of computer circuits shows that the 16th system is the most effective. That it is used in modern machines.
We will consider the system with base 2 effective because of its widespread distribution.
Here are the main considerations in favor of this system:
The latter requires a special explanation. In this case, it is not the time intervals required for performing certain operations, but the speed, determined indirectly by the relative number of operations that are required to perform, for example, division or multiplication in binary or other systems.
If "p" is the base of the number system, then the maximum digit in one digit is (p-1).
If N is the maximum number, then its image requires log p N digits.
In order to perform a multiplication operation, for example, (p-1) * log p N addition operations are required. If we compare this number of operations in the system with the base "p" and relate it to the number of operations in the system with the base "2", then we can get the following function:
(p-1) * log
p
N p-1
___________ _____
f (p) = =
1 * log
2
N log
2
p
| n | 2 | 3 | four | five | 6 | ... | ten |
| f (n) | 1,000 | 1.262 | 1,500 | 1,725 | 1,913 | ... | 2,709 |
These are just basic considerations in favor of choosing the binary number system as the basis. There are others (control, troubleshooting), but we omit them from consideration.
Whenever a numbering system other than the actual numbering system is used for calculations, the translation 10 => p, p => 10 is necessary.
There are systems that give significantly higher speeds, but also require more equipment.
This translation can be done:
In all these cases, different approaches and methods are used in principle. Due to the fact that we will have to prepare information for the program manually, we will consider, first of all, methods aimed at manual translation.
So, we are dealing with a positional number system with the base "p", with natural weights of digits.
Naturally, the decimal system is used as an intermediate one. First, the number is transferred from the system "p" to the 10th, then from the 10th to the system with the necessary base.
We depart from this rule and use the direct translation algorithm from the system with the base "p" to the system with the q command.
Usually, an arbitrary number containing the integral and fractional parts is translated in parts: first, the whole, then the fractional part.
Consider the translation of integers:
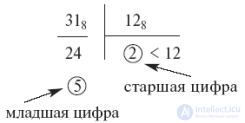
Translation is carried out according to the following rule: the initial number recorded in the system with the base "p" and its quotients are sequentially divided by the number "q" represented in the system "p". The division is made in the system with the base "p" and continues until the result is less than the "q". The first remainder, a smaller "q", gives the highest digit of the number N q . The remainder of the division gives the remaining digits of the number N q .
Example:
31ten
=> 2; 31ten
= 111112
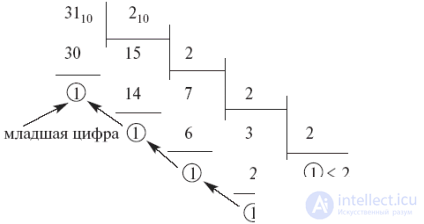
31eight
=> 3; 31eight
= 2213
= 2 * 32
+ 2 * 3one
+ 1 * 30
= 18 + 6 + 1 = 25ten
.
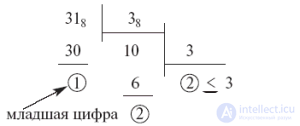
31eight
=> 10; 31eight
= 25ten
.
1111112
=> 10; 1111112
= 63ten
.

The conversion of fractional numbers from a system with a base "p" to a system with a base "q" is performed according to the following rule: the initial number D p is sequentially multiplied by the number "q" recorded in the system "p". Entire parts of the resulting products give "p" -th records of "q" -x numbers, starting with the highest. Multiplication is performed in the system with the base "p" to obtain the required accuracy.
Example:
| 0, |
5314 8 5 8 |
| 3 |
2774 five |
| one |
6754 five |
| four |
2634 five |
| one | 6014 |
| 0, |
318 10 2 10 |
| 0 |
636 2 |
| one |
272 2 |
| 0 |
544 2 |
| one |
088 2 |
| 0 | 176 |
| 0, |
5314 8 12 8 |
|
one five |
2630 314 |
| 6 |
5770 8 12 8 |
|
one five |
3760 770 |
| 7 |
3660 8 12 8 |
|
one 3 |
7540 660 |
| four |
6340
|
Translation of numbers from one number system to another, when one base is an integer degree of another.
As we already know, in a computer the system with the bases 2, 4, 8, 16 finds the greatest application, i.e. systems that are multiples of degree 2. Therefore, it is advisable to consider only the rules for the translation of numbers in these systems. Similar rules will be true for other systems. Suppose that there is some integer N 8 in the 8th system. It can be represented as:
Suppose that in some way we obtained the record of this number as a binary one, that is:
Since the numbers were equal, it turns out the same partial and identical residues:
If we again divide the whole parts by 2 3 = 8, then again we obtain equal partial and equal residues.
At the same time, we see that each octal digit corresponds to its binary equivalent. Therefore, the translation is performed by simply replacing the digits of the octal system with its binary equivalent and vice versa.
Example:
From these examples we see that the higher the base of the number system, the more compact the record.
| b k-2 | b k-1 | b k | a n |
| 0 | 0 | 0 | 0 |
| 0 | 0 | one | one |
| 0 | one | 0 | 2 |
| 0 | one | one | 3 |
| one | 0 | 0 | four |
| one | 0 | one | five |
| one | one | 0 | 6 |
| one | one | one | 7 |
If we multiply the last relations (6.2) by 8, then:
Comments
To leave a comment
Digital devices. Microprocessors and microcontrollers. computer operating principles
Terms: Digital devices. Microprocessors and microcontrollers. computer operating principles