Lecture
As we already know, there are two main ways of representing numbers - fixed and floating point. Most mainframes work with floating-point numbers, while most specialized computers work with fixed-point numbers.
However, a number of machines work with numbers in these two formats.
In general, the method of representing numbers strongly influences the nature of programming. Thus, programming for computers operating in a system with a fixed comma becomes much more complicated, since, in addition to the algorithmic difficulties, this process also requires tracking the position of the comma.
Let's say that the bit grid of the machine has a constant number of digits - n.
When presenting numbers with a fixed comma, they consider that the comma is always before the highest digit, and all the numbers that participate in the calculations are considered to be an absolute value less than one:
| X | <1
We introduce two characteristics of numbers: the range of variation and the accuracy of the representation.
The range of change is characterized by the limits within which the numbers with which the machine operates are located.

Non-zero smallest number:

Thus, the range of numbers with which the computer works is:
| X | min <= | X | <= | X | max
2 -n <= | X | <= 1 - 2 -n
In other words, numbers that go beyond the range of variation cannot be represented in a computer exactly. If a
then such a number is perceived as infinitely large. These two cases correspond to the concepts of machine zero and machine infinity.
With optimal rounding, the absolute error is:

Minimum relative error:
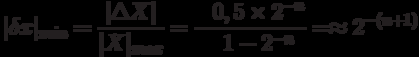
because  with a large "n"
with a large "n"
Maximum relative error:
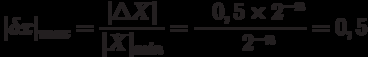
The error in the representation of a number depends on the size of the number itself and the rounding method:

Note that for small numbers the error can reach a large value.
In a floating-point computer, the number is represented as:
X = ± M x * q ± p ,
where: M x - mantissa numbers;
q - the base of the number system;
p - order.
The discharge grid of the machine takes the following form:
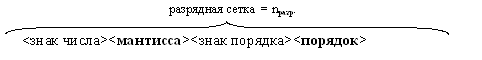
This is only a conditional image of the main syllables in the number. Note that in a real computer any other order of arrangement can be adopted.
Let the "m" digits be reserved for the image of the mantissa, and the "k" digits for the image of the order. Then for the binary system and the normalized form of the number:
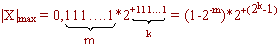
q = 2;
0.1 <= Mx <1 is the normalized mantissa.

That is, the range of numbers:

The absolute error in representing a number in a computer with a floating comma is equal to:

Because
2 -1 <= | M x | <= 1-2 -m
then the minimum relative error:

and the maximum relative error:

It is seen that the relative error in the computer with a floating point does not depend on the order of the number. At the same time, the accuracy of representation of large and small numbers varies slightly.
Theoretically, "floating point" has advantages over "fixed". But the corresponding device is much more complicated. In addition, the specifics of performing floating point operations require a larger number of micro-operations, which leads to a decrease in the speed of the computer. However, the floating point removes the responsibility of the programmer to monitor the position of the comma in calculations and greatly simplifies the process of programming computational problems.
The main feature of various methods of performing arithmetic operations is that any operation (addition, subtraction, multiplication, division, etc.) is reduced to a certain sequence of microoperations, such as:
Addition is performed by the rules of addition of numbers in positional number systems.
That is, this operation is performed in bits, and the transfer that occurs in the lower digits is sent to the higher digits.
Example:
0.101101 1st item
+
0.000101 2nd item
________
0,101000 amount
0,00101 transfer
________
0.100010 amount
0.01 transfer
________
0,110010 amount
The operations of addition are performed simultaneously on all the digits of the two terms and continue as long as there are transfers. Emerging transfers lead to the continuation of the operation. This is one of the features of positional systems. We see that the actual operation of determining the partial sum of the items is performed in one step, and the emerging carry over extends to more and more significant digits.
Shift
There are two types of shear microoperation:
A logical shift leads to the displacement of all digits of a number, including the sign, to the left or to the right. In this case, the discharges are filled with zeros or ones.
The arithmetic shift is performed on a part of the number, a part of the shifted digits is lost. (Obviously, the sign bit should be excluded from consideration).
Broadcast.
This micro-operation assumes that some code (number) is recorded in the corresponding device and supplants the code that was there before transmission.
There are two types of gear:
Transform.
The function performed on the transmitted numbers is called a transform. Inverting code is considered more often than others in arithmetic fundamentals. This is a bitwise micro operation.  which is performed on all digits at the same time.
which is performed on all digits at the same time.
Codes used to represent negative numbers.
The main disadvantage of constructing devices that implement arithmetic operations is the complex nature of the subtraction algorithm. To overcome it in a computer, an operation is always performed by different rules than is usually done. It is based on the addition operation. Algorithms for performing such operations require special codes for representing negative numbers.
Direct code.
This is the natural and most familiar representation of a number as follows:
sign:
"+" corresponds to 0
"-" corresponds to 1
In digital digits, the modulus of a positive or negative number is written.
[X] pc - thus we denote the image of the number "X" in the direct code.
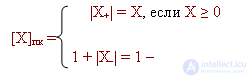
Consider the ranges of numbers being represented:
X + min = 0.000 .... 0 - image of positive zero
X + max = 0.111 .... 1 = 1 - 2 -n
X -min = 1.111 .... 1 = - (1-2 -n )
X -max = 1,000 .... 0 - the image of a negative zero.
Thus, zero has a double image.
Remarks:
[X]PC
* [Y]PC
= sign Z. | Z | | Z | = | X | * | Y |

Due to a number of inconveniences in the computer, subtraction operations, addition of numbers with different signs and divisions in the direct code are practically not performed.
Additional code
An additional code is a code in which “0” is written for a positive number, a number modulus is written in numeric digits, 1 is written in a sign digit, and 1 is added to a numeric digit.
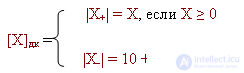
If some X - = -0, x 1 x 2 ... x n needs to be represented in the additional code, then
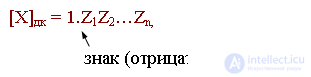
where: 1 - 0, x 1 x 2 ... x n = 0, Z 1 Z 2 ... Z n
The ranges of numbers represented:
X + min = 0.0 ... 0 - positive zero
X + max = 0.11 ... 1 = 1-2 -n is the maximum positive number.
X - min = 1.11 ... 1 = 2-2 -n - the minimum negative number
X - max = 1.0 ... 0 - the largest (modulo) negative number
Thus, zero has a single representation.
Indeed, since
XX = [X + ] dk + [X - ] dk = 0, then in the additional code: | X + | + 10 - | X - | = 10, if there is no second significant digit in the bit grid of the computer, then this overflow is lost, and only zero will be in the significant digit.
An important feature in obtaining an additional code of a negative number is as follows:
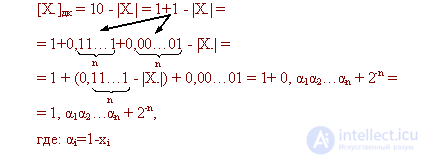
Thus, in order to write an additional code of a negative number, it is necessary to put a unit in the sign bit, invert all the digits of the number and add one to the lower digit. This is also the rule for converting from an additional code to a direct code.
Consider the examples of the operation of adding two numbers with different signs.
The following cases are possible:
It must be remembered that it is impossible, when performing operations, to go beyond the range of numbers represented in this bit grid, written with a comma, represented in this bit grid.
We set n = 3, 1 - the sign digit and 2 - digital.
X+
= 0.10 Y+
= 0.01
In the additional code
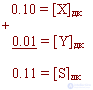
That is, there are no features.
X+
= 0.10 Y-
= -0.01
In the additional code
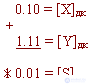
Overflow is lost and you get the right result.
X+
= 0.01 Y-
= -0.11
In the additional code
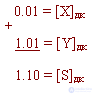
X-
= -0.10 Y-
= -0.01
In the additional code
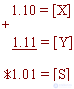
The resulting overflow is lost and the overall result is negative.
Thus, an important feature of the additional code is that the sign bit in the process of performing the operation is considered together with the digital ones. The resulting transfers are lost and do not affect the result of the operation.
Reverse code
The inverse is the code for which a 0 is written in the sign bit of a positive number, the number modulus is written in digital, and 1 is written in a sign digits, the inverted digits of the source number are written in digital digit.

Define the ranges of numbers:
X + min = 0.00 ... 0 - positive zero.
X + max = 0.111 ... 1 = 1 - 2 -n
X - min = 1.11 ... 1 0 = 2 - 2 -n + 1
X - max = 1.00 ... 00 = 1
In the reverse code there are two images of zero:
"Positive" zero:
[X] ok = 0.0 ... 0
and "negative" zero:
[X] ok = 1.11 ... 11
Wherein
X - X = [X
+
]
OK
+ [X
-
]
OK
= | X
+
| + 10 - (10)
-n
- | X
-
| = +10 - (10)
-n
= 0
That is, the transfer unit in the sign bit is equivalent to the lower order unit. Therefore, when performing the operation of addition-subtraction, the resulting transfer must be cyclically added to the lower order of the partial result.
Consider the former four cases, remembering that the sum of the two terms in the module must be less than one.
X+
= 0.10 Y-
= -0.01 X+
+ Y-
= S+
In the reverse code:
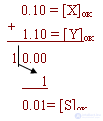
The resulting overflow should be added to the lower part of the partial amount.
X+
= 0.10 Y+
= +0.01 X+
+ Y+
= S+
In the reverse code:

There are no features compared to the direct code.
X+
= 0.01 Y-
= -0.10 X+
+ Y-
= S-
In the reverse code:
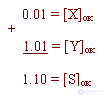
That is, there is no cyclic transfer.
X-
= -0.01 Y-
= -0.10 X-
+ Y-
= S-
In the reverse code:
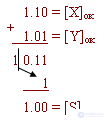
There is an overflow of the sign bit, which is added to the low order of the partial amount.
Note that getting a return code is easier than an additional one. This is a bit-executed code inversion micro-operation. As will become clear from the circuit design, this micro-operation is performed as quickly as the transfer of the code.
Since the result of the operation is a set of results for all digits, this operation can be performed simultaneously on all digital digits of the number.
Comments
To leave a comment
Digital devices. Microprocessors and microcontrollers. computer operating principles
Terms: Digital devices. Microprocessors and microcontrollers. computer operating principles