Lecture
International Olympiad in Informatics, 2000
In some countries, the walls are constructed in such a way that each wall connects exactly two cities, and the walls do not intersect each other. Thus, the country is divided into separate parts. To get from one area to another, you must either pass through the city, or cross the wall. Any two cities A and B can be joined by no more than one wall (one end of the wall in city A, the other in city B). Moreover, there is always a path from city A to city B, passing along any walls and through cities.
There is a club whose members live in cities. In each city can live either one member of the club, or none at all. Sometimes club members have a desire to meet inside one of the regions, but not in the city. To get to the desired area, each member of the club must cross some set of walls, possibly equal to zero. Club members travel by bike. They do not want to enter any city because of heavy traffic on city streets. They also want to cross the minimum possible number of walls, since crossing a wall with a bicycle is quite difficult. Based on this, you need to find such an optimal area so that the total number of walls that club members need to cross, called the sum of intersections, is the smallest of all possible.
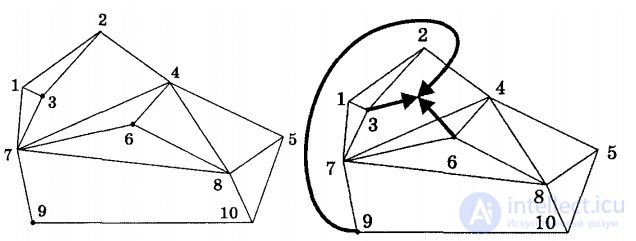
Cities are numbered with integers from 1 to N, where N is the number of cities. In the figure on the right (above), the numbered vertices indicate cities, and the lines connecting the vertices indicate walls. Suppose the club members are three people who live in cities with numbers 3.6 and 9. Then the optimal area and the corresponding routes of the club members are shown in the figure below. The sum of intersections is 2, since club members are required to cross two walls: a person from city 9 needs to cross a wall between cities 2 and 4, a person from city 6 needs to cross a wall between cities 4 and 7, and a person from city 3 does not cross walls at all.
It is required to write a program that, according to given information about cities, regions and places of residence of club members, finds the optimal region and the minimum amount of intersections.
Input
The first line contains one integer: the number of regions M satisfying the inequalities 2 <= M <= 200. The second line contains one integer: the number of cities N, and 3 <= N <= 250. The third line contains one integer: the number of members club L, with 1 <= L <= 30 and L <= N.
The fourth line contains L different integers in ascending order: the numbers of the cities where the club members live.
The rest of the file contains 2M lines, a pair of lines for each of the M regions. The first two lines describe the first area, the second two lines - the second area, and so on. In each pair, the first line contains the number of cities on the border of the area; the second one contains the numbers of these I cities in the order of going around the border clockwise. The only exception is the last area - this is the outside (external) area that surrounds all cities and other areas, and for it the order of the cities on the border is set counterclockwise.
The order of the description of areas in the input file sets the whole numbers of these areas. The area described first in the input file has number 1, described second - number 2, and so on. Note that the input file contains a description of all areas formed by cities and walls, including the outside (external) area.
Conclusion
The first line of this file contains a single integer - the minimum sum of intersections. The second line contains a single integer - the number of the optimal region. If there are several different solutions, you only need to find one of them.
Input Example Output Example 10 2 10 3 3 3 6 9 3 1 2 3 3 1 3 7 four 2 4 7 3 3 4 6 7 3 4 8 6 3 6 8 7 3 4 5 8 four 7 8 10 9 3 5 10 8 7 7 9 10 5 4 2 1
The basic idea is to transform this problem to a problem on the graph as follows: let the vertices be areas formed by the walls. The presence of an edge means the adjacency of areas. To move into the adjacent area you need to climb exactly one wall. For example, for the data from the input example, we obtain a graph of 10 vertices (10 regions) connected by edges (adjacent regions) as follows:
Area Adjacent areas 1 2 3 10 2 1 3 10 3 1 2 4 10 4 3 5 6 10 5 4 6 7 6 4 5 8 7 5 9 10 8 6 9 10 9 7 8 10 10 1 2 3 4 7 8 9
It is necessary to find such a peak on the graph so that the sum of the distances to it from the cities where the club members live is minimal. Each city can be a boundary for several areas. Therefore, for each city you need to choose the most profitable area, among its boundary areas.
To establish the fact of adjacency of areas, the following algorithm is used. If the lists of cities bordering regions (t [i] and t [j]) include 2 identical cities, then these areas are adjacent, since they have a common wall connecting these two cities.
To realize the fact that there are two common numbers, two arrays are used, which contain 1 in the positions of the cities bounding the region, and 0 in all other positions. If units are found in both areas on the same positions more than two times, then the areas are adjacent.
Using the Floyd algorithm, we find the shortest distances G [i, j] on the constructed graph between all pairs of vertices (i, j).
Next cycle in all areas we find the minimum cost of the collection of club members in it and among these values we find the minimum and the number of the corresponding area. For each member of the club, as an area from which he will travel, you need to consistently select all areas adjacent to the city, remembering the one that has the shortest path to the current gathering place.
Walls ()
1. Read from the file information about the area, take the area vertices
count.
2. Until all pairs of areas have been processed, repeat clauses 2.1-2.4:
2.1. Initialize the number of common zero cities.
2.2. Go through all the cities. If the city belongs to both regions, then
increase the number of common cities by 1.
2.3. If there is more than one common city for the current pair
of regions, then connect vertices-regions by an edge.
2.4. Go to the next pair of areas.
3. Use the Floyd-Worshell algorithm to find the distances between
all pairs of areas (perform paragraphs 3.1-3.2):
3.1. Initialize distances to infinity.
3.2. For each three areas, repeat paragraphs. 3.2.1-3.2.2:
3.2.1. If the length of the path from the first to the second region through the third
less than from first to second, then assume that the path through
the third peak is minimal.
3.2.2. Go to the next three areas.
4. Select the first area.
5. Until all the areas have been reviewed, repeat paragraphs. 5.1-5.3:
5.1. Find the sum of distances from areas where club members live to
current region, while choosing the optimal region for
club members.
5.2. If the sum to the current vertex is less than the minimum, then take
This amount is minimal, and the current area is optimal.
5.3. Go to the next area.
6. Print the number of the optimal area and the sum of the distances to it.
Comments
To leave a comment
Algorithms
Terms: Algorithms