Lecture
Dynamic programming in control theory and the theory of computing systems is a way to solve complex problems by breaking them down into simpler subtasks. It is applicable to problems with an optimal substructure ( English ), which looks like a set of overlapping subtasks, the complexity of which is slightly less than the initial one. In this case, the computation time, compared with the “naive” methods, can be significantly reduced.
The key idea in dynamic programming is quite simple. As a rule, to solve the problem, it is required to solve separate parts of the problem (subtasks), and then combine the solutions of the subtasks into one common solution. Often, many of these subtasks are the same. The dynamic programming approach is to solve each subtask only once, thereby reducing the number of calculations. This is especially useful in cases where the number of recurring subtasks is exponentially large.
The method of dynamic programming from above is simply memorizing the results of solving those subtasks that can be re-encountered later. Dynamic programming from below involves the reformulation of a complex task as a recursive sequence of simpler subtasks.
The phrase "dynamic programming" was first used in the 1940s by R. Bellman to describe the process of finding a solution to a problem, where the answer to one problem can be obtained only after solving the problem "preceding" it. In 1953, he clarified this definition to modern. Initially, this area was founded, as a system analysis and engineering, which was recognized by IEEE. Bellman's contribution to dynamic programming was perpetuated in the title of the Bellman equation, the central result of dynamic programming theory, which reformulates the optimization problem in a recursive form.
The word “programming” in the phrase “dynamic programming” in reality has almost nothing to do with “traditional” programming (code writing) and it makes sense as in the phrase “mathematical programming”, which is synonymous with the word “optimization”. Therefore, the word “program” in this context rather means the optimal sequence of actions for obtaining a solution to the problem. For example, a certain schedule of events at an exhibition is sometimes called a program. The program in this case is understood as a valid sequence of events.

The optimal substructure in dynamic programming means that the optimal solution of smaller subtasks can be used to solve the original problem. For example, the shortest path in a graph from one vertex (denoted by s) to another (denoted by t) can be found as follows: first, consider the shortest path from all vertices adjacent to s to t, and then, taking into account the weights of the edges that s are connected to with adjacent vertices, choose the best path to t (through which vertex it is best to go). In general, we can solve the problem in which there is an optimal substructure, doing the following three steps.
Subtasks are solved by dividing them into even smaller subtasks, and so on, until they arrive at a trivial case of a problem that can be solved in constant time (the answer can be said right away). For example, if we need to find n!, Then the trivial task will be 1! = 1 (or 0! = 1).
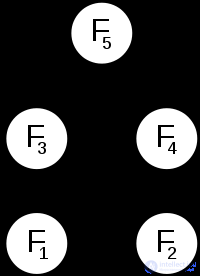
Overlapping subtasks in dynamic programming mean subtasks that are used to solve a number of problems (not one) larger (that is, we do the same thing several times). A prime example is the calculation of the Fibonacci sequence, 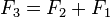 and
and 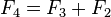 - even in such a trivial case of calculating only two Fibonacci numbers, we have already calculated
- even in such a trivial case of calculating only two Fibonacci numbers, we have already calculated 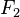 twice. If you continue further and count
twice. If you continue further and count 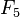 then
then 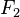 will count two more times, so as to calculate
will count two more times, so as to calculate 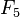 will be needed again
will be needed again 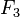 and
and 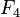 . It turns out the following: a simple recursive approach will spend time on calculating solutions for problems that it has already solved.
. It turns out the following: a simple recursive approach will spend time on calculating solutions for problems that it has already solved.
To avoid such a course of events, we will save the decisions of the subtasks that we have already solved, and when we again need a solution of the subtasks, instead of calculating it again, we simply remove it from memory. This approach is called caching. Further optimizations can be done - for example, if we are sure that we no longer need a solution to a subtask, we can throw it out of memory, freeing it for other needs, or if the processor is idle and we know that a solution to some not yet counted subtasks, we will need in the future, we can solve them in advance.
Summarizing the above, we can say that dynamic programming uses the following properties of the problem:
Dynamic programming usually takes two approaches to solving problems:
Programming languages can memorize the result of a function call with a specific set of arguments (memoization) in order to speed up the “calculation by name”. In some languages, this feature is built in (for example, Scheme, Common Lisp, Perl), and in some it requires additional extensions (C ++).
Serial dynamic programming, which is included in all textbooks on operations research, and non-serial dynamic programming (NSDP), which is currently poorly known, although it was discovered in the 1960s, are known.
Normal dynamic programming is a special case of non-serial dynamic programming, where the graph of the relationship of variables is just a way. The NSDP, being a natural and general method for accounting for the structure of an optimization problem, considers the set of constraints and / or the objective function as a recursively computable function. This allows you to find a solution in stages, at each of the stages using the information obtained at the previous stages, and the effectiveness of this algorithm directly depends on the structure of the graph of the relationship of variables. If this graph is sufficiently sparse, then the amount of computation at each stage can be kept within reasonable limits.
One of the main properties of problems solved by dynamic programming is additivity. Nonadditive problems are solved by other methods. For example, many of the tasks for optimizing a company's investment are non-additive and are solved by comparing the value of a company with and without investment.
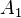 , ...,
, ..., 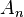 , it is required to minimize the number of scalar operations for their multiplication.
, it is required to minimize the number of scalar operations for their multiplication.
Comments
To leave a comment
Algorithms
Terms: Algorithms