Lecture
The Floyd-Worshell algorithm is a dynamic algorithm for finding the shortest distances between all vertices of a weighted directed graph. Designed in 1962 by Robert Floyd and Stephen Worshell.
A more rigorous formulation of this problem is as follows:
there is a directed graph G = (V, E) to each arc v -> w of this graph the nonnegative cost C [v, w] is associated. The general problem of finding the shortest paths is to find for each ordered pair of vertices v, w) any path from the vertex v to the vertices w whose length is minimal among all possible paths from v to w.
For definiteness, we assume that the vertices of the graph are sequentially numbered from 1 to n. Floyd's algorithm uses a matrix A of size n * n, in which the lengths of the shortest paths are calculated. First A [i, j] = C [i, j] for all i! = J. If the arc i - »j is absent, then C [i, j] = infinity. Each diagonal element of matrix A is 0.
Over matrix A, n iterations are performed. After the kth iteration, A [i, j] contains the value of the shortest path length from vertex i to vertex y that do not pass through vertices with a number greater than k. In other words, between the end vertices of the path i and y there can be only vertices whose numbers are less than or equal to k. At the kth iteration, the following formula is used to calculate the matrix A:
A k [i, j] = min (A k-1 [i, j], A k-1 [i, k] + A k-1 [k, j])
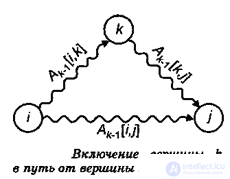
The subscript k denotes the value of matrix A after the kth iteration, but this does not mean that there are n different matrices, this index is used to shorten the record. To calculate A k [i, j], compare the value of A ki [i, j] (i.e. the cost of the path from vertex i to vertex j without the participation of vertex k or another vertex with a higher number) with the value of A k-1 [i, k] + A k-1 [k, j] (the cost of the path from the vertex i to the vertex k plus the cost of the path from the vertex k to the vertex j). If the path through vertex k is cheaper than A k-1 [i, j], then the value of A k [i, j] changes.
The execution time of this program, obviously, is of the order of 0 (V 3 ), since there is practically nothing in it except the three cycles nested in each other. The proof of the "correctness" of this algorithm is also obvious and is carried out using mathematical induction on k, showing that at the k-th iteration, the vertex k is included in the path only when the new path is shorter than the old one.
The most commonly used name, the method received in honor of two American researchers, Robert Floyd and Stephen Worshelle, who simultaneously discovered it in 1962. Other options are less common: the Roy-Worshell algorithm or the Roy-Floyd algorithm. Roy is the name of the professor who developed a similar algorithm 3 years earlier than his colleagues (in 1959), but this discovery remained unknown. The Floyd-Worshell algorithm is a dynamic algorithm for calculating the shortest path values for each of the vertices of the graph. The method works on weighted graphs, with positive and negative edge weights, but without negative cycles, being thus more general in comparison with the Dijkstra algorithm, since the latter does not work with negative edge weights, and besides, its classical implementation involves the determination of optimal distances from one vertex to all others.
To implement the Floyd – Warshell algorithm, we form the adjacency matrix D [] [] of the graph G = (V, E), in which each vertex is numbered from 1 to | V |. This matrix has the size | V | ´ | V |, and each of its elements D [i] [j] is assigned the weight of an edge that goes from the vertex i to the vertex j. As the algorithm runs, this matrix will be overwritten: a value will be entered into each of its cells, which determines the optimal path length from vertex i to vertex j (the rejection of allocating a special array for this purpose will save memory and time). Now, before compiling the main part of the algorithm, it is necessary to understand the contents of the shortest path matrix. Since each of its D [i] [j] elements must contain the smallest available route, we can immediately say that for a single vertex it is zero, even if it has a loop (negative cycles are not considered), therefore, all elements of the main diagonal ( D [i] [i]) must be reset. And so that zero off-diagonal elements (the adjacency matrix could have zeros in those places where there is no direct edge between vertices i and j), if possible, change their value, we define them equal to infinity, which in the program can be, for example, the maximum possible long path or just a large number.
The key part of the algorithm, consisting of three cycles, an expression and a conditional operator, is written fairly compactly:
For k from 1 to | V | perform
For i from 1 to | V | perform
For j from 1 to | V | perform
If D [i] [k] + D [k] [j]
The shortest path from the vertex i to the vertex j can pass as soon as through them, or through the set of other vertices k∈ (1, ..., | V |). The optimal path from i to j is either the path not passing through k or passing through. To conclude that there is a second case, it means to establish that such a path goes from i to k, and then from k to j, and therefore must replace the value of the shortest path D [i] [j] with the sum of D [i] [k] + D [ k] [j].
Consider the full code of the Floyd-Worshell algorithm in C ++ and Pascal, and then analyze in detail the sequence of actions performed by it.
|
#include "stdafx.h"
#include using namespace std; const int maxV = 1000; int i, j, n; int GR [maxV] [maxV]; // Floyd-Worshel algorithm void FU (int D [] [maxV], int V) { int k; for (i = 0; i for (k = 0; k for (i = 0; i for (j = 0; j if (D [i] [k] && D [k] [j] && i! = j) if (D [i] [k] + D [k] [j] D [i] [j] = D [i] [k] + D [k] [j]; for (i = 0; i { for (j = 0; j cout << endl; } } // main function void main () { setlocale (LC_ALL, "Rus"); cout << "The number of vertices in the column>"; cin >> n; cout << "Enter the edge weights matrix: \ n"; for (i = 0; i for (j = 0; j { cout << "GR [" << i + 1 << "] [" << j + 1 << "]>"; cin >> GR [i] [j]; } cout << "The shortest path matrix:" << endl; FU (GR, n); system ("pause >> void"); } |
| one 2 3 four five 6 7 eight 9 ten eleven 12 13 14 15 sixteen 17 18 nineteen 20 21 22 23 24 25 26 27 28 29 thirty 31 32 33 34 35 36 37 38 39 40 41 |
program Floyd_Uorshell;
uses crt; const maxV = 1000; type matr = array [1..maxV, 1..maxV] of integer; var i, j, n, inf: integer; GR: matr; {Floyd-Warshell algorithm} Procedure FU (D: matr; V: integer); var k: integer; begin inf: = 1,000,000; for i: = 1 to V do D [i, i]: = 0; for k: = 1 to V do for i: = 1 to V do for j: = 1 to V do if (D [i, k] <> 0) and (D [k, j] <> 0) and (i <> j) then if (D [i, k] + D [k, j] D [i, j]: = D [i, k] + D [k, j]; for i: = 1 to V do begin for j: = 1 to V do write (D [i, j]: 4); writeln; ; end; end; {main program block} begin clrscr; write ('Number of vertices in the column>'); readln (n); writeln ('Enter the edge weights matrix:'); for i: = 1 to n do for j: = 1 to n do begin write ('GR [', i, '] [', j, ']>'); read (GR [i, j]); end; writeln ('Matrix of the shortest paths:'); FU (GR, n); end. |
Suppose that, as an adjacency matrix, each element of which stores the weight of a certain edge, the following matrix was defined:
| 0 | 9 | 2 |
| one | 0 | four |
| 2 | four | 0 |
The number of vertices in the graph, the representation of which is a given matrix, is 3, and, moreover, there is an edge between every two vertices. This is the graph itself:
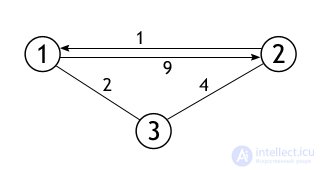
The task of the algorithm is to rewrite this matrix so that each cell, instead of the weight of the edge from i to j, contains the shortest path from i to j. For example, a very small graph is taken, and therefore there will be nothing surprising if the matrix retains its original state. But the result of testing the program shows the replacement of two values in it. The following diagram will help with the analysis of this particular example.

This table shows the 27 steps for performing the main part of the algorithm. They are so many for the reason that the execution time of the method is O (| V | 3 ). Our graph has 3 vertices, and 3 3 = 27. The first replacement occurs at the iteration, at which k = 1, i = 2, and j = 3. At that moment, D [2] [1] = 1, D [1] [3] = 2, D [2] [3] = 4. The condition is true, that is, D [1] [3] + D [3] [2] = 3, and 3 <4, therefore, the element of the matrix D [2] [3] receives a new value. The next step, when the condition also truly introduces changes to the element located at the intersection of the second row and third column.
Comments
To leave a comment
Algorithms
Terms: Algorithms