Lecture
Just as a roadmap can be modeled with a directed graph, in order to find the shortest path from one point to another, a directed graph can be interpreted as a kind of transport network and used to solve problems of substance flows in a pipeline system.
Each oriented edge of the network can be considered as a channel through which the product moves. Each channel has a predetermined throughput , which characterizes the maximum speed of product movement through the channel, for example, 200 liters of fluid per minute for a pipeline or 20 amperes for a wire of an electrical circuit. The vertices are the points of intersection of the channels ; through the tops, different from the source and drain, the product passes without accumulating. In other words, the rate at which a product reaches a peak should be equal to the rate at which it is removed from the top.
In the problem of the maximum flow, we want to find the maximum transfer rate of the product from the source to the drain, at which bandwidth limitations will not be violated. The main methods used in the algorithms for solving problems on the maximum flow can be used to solve other problems associated with transport networks.
Let a non-oriented graph G = (V, E) be given. 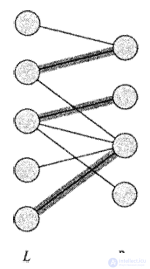 A matching is a subset of edges M є E such that, for all vertices v є V, M contains at most one edge incident to v.
A matching is a subset of edges M є E such that, for all vertices v є V, M contains at most one edge incident to v.
We confine ourselves to the task of searching for maximal matching in bipartite graphs . We assume that the set of vertices can be divided into two subsets V = LUR, where L and R do not intersect, and all edges from E are between L and R. Further we assume that each vertex from V has at least one incident edge.
The task of finding the maximum matching in a bipartite graph has many practical applications. As an example, consider the matching of a set of machines L and a set of tasks R, which must be performed simultaneously. The presence in E of the edge (u, v) means that the machine u є L can perform the task v є R. The maximum matching ensures the maximum load of the machines.
This section describes the classic Ford-Fulkerson method for finding the maximum flow. As an application of this method, a maximum match is searched for in an undirected bipartite graph.
Comments
To leave a comment
Algorithms
Terms: Algorithms