Game (solution through graphs)

Belarussian Olympiad in Informatics, 2001

The task

Known to the whole of Mogilev, the company released a game for which a construction consisting of small platforms and pipes is necessary. Platforms are divided into starting (their N1 pieces), finishing (N3 pieces) and intermediate (N2 pieces). All launch platforms are at the same height. Finishing platforms are also at the same height. All heights of intermediate platforms are different. They are less than the height of the starting, but more than the height of the finish.

Each platform corresponds to a unique number from 1 to Nl + N2 + N3. The numbering is as follows: all starting platforms are listed first, then intermediate ones and, finally, finishing ones. All intermediate platforms are numbered in descending order of height. That is, if the height of the intermediate platform A is greater than the height of the platform B, then the number A is less than the number B.

There is a ball on each of the launch platforms. The ball can roll from platform A to platform B if they are connected by a pipe and height A is greater than height B. There can be no more than one ball on each of the finishing platforms. If the ball is on a certain platform, the player can choose the direction of the further path of the ball, that is, choose the platform on which the ball will roll. Also for each intermediate platform, a number C is set equal to the maximum number of balls that can roll on it during the game. The goal of the game is to ensure that as many balls appear on the finishing platforms.

You need to know what the maximum number of balls can be on the finishing platforms as a result of the game.

Input

The Game.in input file contains design information in the following form:

  N1 N2 N3 
 CN1 + 1 
 ..
 CNl + N2 
 K1 A [1.1]: A [1.K1] 
 K2 A [2.1]: A [2.K2] 
 ..
 KNl + N2A [Nl + N2.1]: A [Nl + N2.KNl + N2] 

where the numbers N1, N2, N3 are respectively the number of starting, intermediate and finishing platforms. Cj - the maximum number of balls that can ride on an intermediate platform with the number j (N1 + 1 <= j <= N1 + N2) for the entire game. Ki is the number of pipes leaving the platform with the number i (1 <= i <= N1 + N2).

The elements of array A listed in the row are the numbers of the platforms on which the ball can slide from the corresponding platform.

Limitations:
All numbers are integers.

  0 <N1.  N2.  N3 <51 
 1 <Nl + N2 + N3 <201 
 0 J Cj J 50 

There are no pipes between the launch platforms. There are no pipes between the finishing platforms.

Conclusion

The first line should contain a single number equal to the maximum number of balls that may be on the finishing platforms as a result of the game.

  Input Example Output Example
 3 4 3 2 
 3 
 2 
 one 
 2 
 14 
 14 
 14 
 2 5 6 
 1 7 
 1 7 
 3 8 9 10 

Solution [up]

Starting, intermediate and finishing platforms are naturally represented by the vertices of the graph, and the pipes between them are arcs. However, this task is slightly different in its formulation from the classical one, since the vertex weight is given here: “... for each intermediate platform, a number C is set equal to the maximum number of balls that can roll through it during the game” . To go to the classical formulation, it is enough to replace such vertices with arcs. In this case, the entered arcs are assigned the weight of the replaced vertices. It is clear that additional vertices should appear.

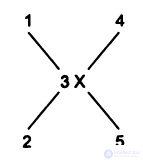
For example, let two arcs (1 -> 3 and 2 -> 3) and two arcs (3 -> 4 and 3 -> 5) go to vertex 3 with weight X, as shown in the figure. We add vertex 6 and arc 3 -> 6 with weight X.

As the intermediate platforms turn into arcs, then the total number of vertices increases by N2, where N2 is the number of intermediate platforms.

Add a source and associate it with the vertices corresponding to the launch platforms. The throughput of the arcs is 1, since according to the condition of the problem there is a ball on each of the launch platforms.

For each intermediate platform with the number /, we add two vertices with the numbers N1 + i and all + i (where all = N1 + N2 + N3), respectively. We also add an arc between these vertices with the bandwidth of the vertex.

All incoming arcs from the launch platforms will be built at the vertices M + i. Under the terms of the task, their throughput is not limited. All arcs from intermediate platforms will be built from all + i vertices - their throughput is also unlimited.

Add a top-runner with arcs to it from all finishing platforms. The weights of these arcs are equal to 1, since on each of the finishing platforms there can be no more than one ball.

To output the answer to the question “What is the maximum number of balls can be on the finishing platforms as a result of the game?”

The initial graph for the problem from the example.

Task graph after conversion (bandwidth indicated above edges)

Formal description

  Game ()
 1. Read the task input data from the file.
 2. Create a graph in which the vertices are platforms.  Tie the vertices that
    connected by pipes.
 3. Create for each intermediate platform create a top and link it
    with vertices with which the current vertex was connected.
 4. Associate the current intermediate node with the created one.  Throughput 
    the ability to set equal to the constraint for the current vertex.
 2. Create a vertex-source and connect it with the vertices of the graph, which
    meet launch platforms.  Bandwidth for these edges
    equals one.
 3. Create a top-drain and connect it to the finishing platforms. 
    The bandwidth of the ribs is 1.
 4. Find the maximum flow algorithm Ford-Fulkerson 
    between the source and drain.
 5. Calculate the flow between the source and the launch platforms and output it.