Lecture
This article will examine the problem on the graphs about the possibility of drawing a particular graph without self-intersections. That is, draw a graph so that its edges do not have common interior points. The task is usually called the problem of flat-laying graph .
The scope of the result that we get is very extensive. One of them is the manufacture of electronic circuits. Electrical circuits are printed on the board made of insulating material. Since the applied chains are not isolated, they should not intersect. This raises the question of how to arrange the contacts on the diagram so that you can apply chains to the board without intersections. And if it is impossible to do that, then how can the minimum number of boards ( layers of the graph) be bypassed.
We will touch only the first part of the question and answer when and how you can draw a graph without self-intersections.
A flat graph is a graph drawn in such a way that its edges do not intersect. It is said that a graph admits flat packing if it can be drawn as flat. Also, flat graphs are called planar .
The graph shown in Fig. 1, flat:

There are non-planar graphs. In fig. 2 shows two such graphs: a full five-vertex and a full bipartite graph. For them there are special designations: K 5 and K 3,3, respectively.
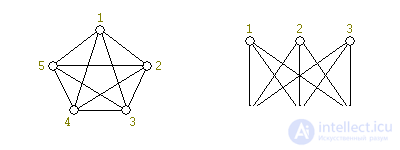
A bipartite graph is a graph whose vertices are divided into two segments (parts), and the edges pass only between the vertices from different parts.
In a planar graph, one can speak not only about vertices and edges, but also about faces.
A face is a part of a plane surrounded by a simple cycle and not containing within itself other elements of the graph.
The outer face is the whole plane surrounding a flat graph.
Task. Determine whether the graph is planar, and, if so, then flatten it.
Comment. If an arbitrary number of vertices of degree 2 is applied to the edges of the planar graph, then it will remain planar; equally, if we put vertices of degree 2 on the edges of a non-planar graph, it will not become planar.
In the late 1920s, Kuratovsky in Poland and L.S. Pontryagin in the USSR independently proved a striking theorem, showing that it prevents the graph from being planar.
A graph is planar if and only if it does not contain K 5 and K 3,3 as its parts (perhaps with additional vertices of degree 2).
We omit the rather complicated proof of this theorem. An interested reader will be able to find it in [2]. However, one should not think that since there are only two difficulties, there are few non-planar graphs: as the number of vertices grows, almost all the graphs are nonplanar.
The considered criterion is very laborious for verification and therefore is of theoretical interest only.
For flat laying of the graph and passing the test whether it is planar, it is convenient to use the gamma algorithm .
At the entrance are graphs with the following properties:
If property (1) is violated, then the graph must be laid separately for the components of the connectivity.
If property (2) is violated, then the graph is a tree and it is trivial to draw its flat packing.
The case of violation of property (3) will be considered in more detail. If there are bridges in the graph, then they need to be cut, to carry out the flat packing of each connected component separately, and then to connect them with bridges. Here a difficulty may arise: in the process of laying, the terminal vertices of the bridge can hide inside a flat graph. We draw one connected component and we will attach others to it in series. Each new connected component will be drawn in the face in which the terminal vertex of the corresponding bridge lies. Since the connectivity graph by bridges of the connected components is a tree, we will be able to obtain a flat packing.
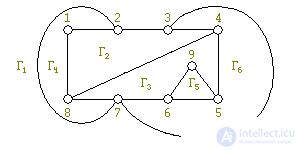
First, we present the algorithm on a specific example. Let a graph G be given (see Fig. 3).
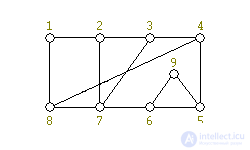
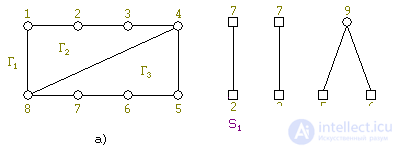
The algorithm is initialized as follows: select any simple cycle; in our example, {1, 2, 3, 4, 5, 6, 7, 8} and we get two faces: Γ 1 - external and Γ 2 - internal (see. Fig. 4).

Denote the selected cycle as G ′. At each step we will build many segments . Each segment S relative to the already constructed graph G ′ is one of two things:
Those vertices that simultaneously belong to G ′ and to some segment are called contact . For our example, the segments and vertices are shown in Fig. 5. Contact vertices are circled in a square.

If there were no contact vertices in any segment, then the graph would not be connected before cutting; if there was only one, then the graph would have a bridge. These possibilities are excluded in advance, so that each segment has at least two contact vertices. Therefore, in each segment there is a chain between any pair of such vertices.
If all contact vertices of a segment S have the numbers of vertices of some face Γ, then we will say that the face Γ contains this segment and denote S ⊂Γ. Maybe there is not one such face containing the segment S , the set of such faces is denoted by Γ ( S ), and their number | Γ ( S ) |.
The general step of the algorithm is as follows: all the segments S i are surveyed and the numbers | Γ ( S i ) | are determined. If at least one of them is 0, then the graph is not planar, the end. Otherwise, choose a segment for which the number | Γ ( S ) | minimal, or one of many, if there are several such segments. In this segment, we find a chain between two contact vertices and put it into any of the faces of the set Γ ( S ), combining the contact vertices of the segment with the corresponding vertices of the face. In this case, this face will be divided into two. The already laid part of the graph G ′ will increase by the number of edges and vertices, and the segment from which the chain is removed will disappear or break up into smaller ones with new contact vertices leading to the vertices of G ′.
As a result of repeating the common pitch, either a flat packing will be obtained when the set of segments becomes empty, or it is received that the graph G is not planar.
Let's return to our example. For now, for any i : S i ⊂ {Γ 1 , Γ 2 }, | Γ ( S i ) | = 2. Therefore, take the first segment by number S i and the first available chain {4, 8}; we insert this chain into the face Γ 2 . We obtain an increased part of G ′ and a reduced system of segments (see Fig. 6 a, b).
Determine which faces accommodate new segments. Now the segments S 1 and S 2 fit only into one face Γ 1 , while the segment S 3 fit into two faces Γ 1 and Γ 3 . Therefore, we take S 1 . Take a chain in it between contact vertices, for example, {2, 7}, and put it in Γ 1 . We obtain an enlarged part of G ′ and a reduced system of segments (see Fig. 7 a, b).
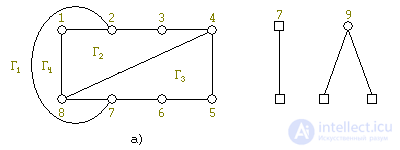
Continuing in this way, we end up with a flat packing G (see Fig. 8).
Once again we describe the gamma algorithm compactly and consider its justification.
Gamma algorithm
We first prove a series of auxiliary assertions.
For any segment | Γ ( S ) | ≤ 2.
Evidence. Indeed, if all the contact vertices of one segment belong to some face Γ (more precisely, the cycle surrounding this face), then they can all belong to only one other face, namely internal or external. Ch.d.
We call the segments S 1 and S 2 conflicting with respect to the already laid part , if:
The conflicting segments S 1 and S 2 have the following property: if | Γ ( S 1 ) | = 2 and | Γ ( S 2 ) | = 2, then Γ ( S 1 ) = Γ ( S 2 ).
Evidence. Indeed, otherwise, having, by definition, one common containing face Γ 3 , they would still have along their own containing face Γ 1 and Γ 2, respectively. Then any chains from S 1 and S 2 could fit in Γ 1 and Γ 2, respectively, and hence in Γ 3 , without intersection; therefore, S 1 and S 2 would not be conflicting. Contradiction. The lemma is proved.
Comment. From the proven lemma, it follows that, having a segment S 1 , and another S 2 segment conflicting with S 1 , then an S 3 segment conflicting with S 2 (but not with S 1 ), and so on, each containing two face, then these faces are common to all segments of the sequence, and you can place the chain L 1 from S 1 to the first face Γ 1 , L 2 from S 2 to Γ 2 , L 3 from S 3 again to Γ 1, and so on. end of sequence. If the chain of segments closes into a cycle of even length, then there will be no problems; if in an odd cycle, then at the end it turns out that two conflicting segments need to be placed without intersections into a common face, which is impossible.
Now we will need as an auxiliary statement the Koenig theorem, which is useful in solving many other problems.
In a graph, all cycles are even if and only if the graph is bipartite.
Evidence.
Adequacy. Consider a bichromatic graph. Start the cycle in the upper lobe. It is necessary to go through an even number of ribs in order to rise again to the upper lobe. Therefore, when closing the cycle, the number of edges will be even.
Need. If the graph is disconnected, then we carry out the proof separately for each component. Let the graph be connected and all its cycles are even. Select an arbitrary vertex v 0 and find arbitrary chains between v 0 and all the other vertices (for example, the shortest Dijkstra algorithm). If one chain ( v 0 , v i ) is of odd length, then any chain ( v 0 , v i ) is odd, otherwise these chains would form an odd cycle. Similarly, if ( v 0 , v i ) is even, then any ( v 0 , v i ) is even. We divide the vertices into two parts: the vertex v 0 and all that are from v 0 at an even distance will enter into one; in the other part, we place all vertices that are at odd distance from v 0 . If the vertices u 1 and u 2 belong to the same lobe, then there can be no edge between them, otherwise this edge together with the chains ( v 0 , u 1 ) and ( v 0 , u 2 ) would form an odd cycle. Ch.d.
Partial packing of the G ′ of a planar graph G is a graph that can be obtained from some packing of the graph G on the plane by removing some edges and vertices. Thus, partial styling is the right start of styling, no errors have been made in it yet.
In a partial packing G ′, we associate each segment with a vertex in some extraneous service graph A ( G ′), where vertices are connected by edges if the corresponding segments are conflicting.
If the result of a step of the gamma algorithm is a partial packing G ′ of a planar graph G such that | Γ ( S ) | = 2 for any segment S with respect to G ′, then A ( G ′) is a bipartite graph.
Evidence. If A ( G ) is not bipartite, then by the Koenig theorem there is an odd-length cycle in it. By Lemma 2, all the vertices of this cycle contain exactly two faces. Since the cycle is odd, we can not put these segments in two faces. Contradiction. The lemma is proved.
Well, we finally come to proving the desired theorem.
The gamma algorithm is correct, that is, if G is a planar graph, then the result of each step of the gamma algorithm is a partial packing G ′.
Evidence. We prove by induction on the number of steps.
The base of induction is obvious: the result of initialization is flat packing, since the laid cycle will be in any packing.
Suppose that the graph G ′ k −1 obtained at the ( k −1) st step is a partial packing. At the current step, the chain L will join it: G ′ k = G ′ k −1 L. Let us prove that the graph G ′ k is also a partial packing. Among the segments at the current step there is no S such that | Γ ( S ) | = 0, otherwise G ′ k −1 would not be partial stacking. Hence, either there exists S such that | Γ ( S ) | = 1, or all S are such that | Γ ( S ) | = 2.
The first case means that the packing of S in Γ is inevitable, so that the graph G ′ k after adding a chain from S remains partial packing. In the second case, we construct the graph A ( Gk − 1 ); by Lemma 3, it is bipartite. Take its connected component A ′; this graph is also bipartite. For segments from A ′, there are exactly two faces Γ 1 and Γ 2 enclosing them. Scatter the segments A ′ on the faces Γ 1 and Γ 2 alternately. This must be done in each partial installation, therefore a partial installation is obtained.
In fact, the basis of the last part of the proof was that if the graph A ( G ′ k −1 ) is bipartal, then after removing some edges and vertices, the graph A ( G ′ k ) is also bipartite. Thus, as a result of each iteration for the planar graph, the partial stacking increases, at the end we get flat stacking.
Comments
To leave a comment
Algorithms
Terms: Algorithms