Lecture
Kruskal algorithmThe Kruskal algorithm is an algorithm for constructing a minimum spanning tree of a weighted connected non-oriented graph. The algorithm was first described by Joseph Kruskal in 1956. The Kruskal algorithm finds a safe edge to add to the growing forest by searching for the edge ( u , v ) with the minimum weight among all the edges connecting two trees in the forest. Denote two trees connected by an edge ( u , v ) as С 1 and С 2 . ( u , v ) - safe for C 1 edge. Kruskal's algorithm is greedy , because at every step it adds an edge to the forest with the minimum possible weight. The implementation of the Kruskal algorithm resembles an algorithm for computing connected components. It uses a structure to represent disjoint sets . Each set contains tree nodes in the current forest. The Find_Set ( u ) operation returns a representative element of the set containing u . Thus, we can determine whether two vertices u and v belong to the same tree by checking the equality of FindJSet ( u ) and Find_Set ( v ). The union of trees is performed using the Union procedure. Formal description
MST_Kruskal (G, w)
1 A "is an empty set
2 for (For) each vertex v є V [G]
3 do Make_Set ( v )
4 Sort the edges from E in a non-decreasing order of their weights w
5 for (For) each ( u, v ) GE (in order of increasing weight)
6 do if Find_Set ( u )! = Find_Set ( v )
7 then A "- A unite with {( u, v )}
8 Union ( u, v )
9 return A
In lines 1-3, the initialization of the set A with an empty set is performed and | V | trees, each of which contains one vertex. The edges in E in row 4 are sorted according to their weight in a non-decreasing order. The for loop in lines 5-8 checks for each edge ( u, v ) whether its ends belong to the same tree. If so, then this edge cannot be added to the forest without creating a loop, so in this case the edge is discarded. Otherwise, when the ends of the edges belong to different trees, in line 7, the edge ( and, y ) is added to the set A, and the vertices of the two trees are combined in line 8. Complexity assessmentThe running time of the Kruskal algorithm for the graph G = (V, E) depends on the implementation of the data structure for disjoint sets. We assume that the forest of non-intersecting sets is implemented with heuristics for union by rank and path compression, since asymptotically this is the fastest known implementation. Initialization of the set A in line 1 takes O (1) time, and the time required to sort the set in line 4 is O (E * lgE) (the cost | V | of Make_Set operations in the for loop in lines 2-3 is taken into account later). The for loop in lines 5-8 performs O (E) Find_Set and Union operations on a forest of disjoint sets. Together with | V | With Make_Set operations, this operation takes O (((V + E) * a (V)) time, where a is a very slowly growing function. Since we assume that G is a connected graph, the relation | E | > = | V | - 1, so operations on non-intersecting sets require O (E * a (V)) time. In addition, since a (| V |) = O (lgV) = O (lgE), the total running time of the Kruskal algorithm is O (E * lgE). Note that | E | <| V | 2 , therefore lg | E | = O (lg V) and the running time of the Kruskal algorithm can be written as O (E * lg V). ExampleExecution of the Kruskal algorithm: 1. The initial phase. Minimum forest cover is empty. 2. Enumerate the edges in order of increasing weight: the first edge with weight 2. Add it to A. 3. The next safe edge with weight 6. Add it. 4-8. Add the rest of the safety edges. Ribs weighing 17, 19, and 25 are not safe. Their ends are in the same connected component. A rib with a weight of 21 is safe, so we add it. Minimum spanning tree built. |
1. sort the edge scales
2. choose the minimum that does not form cycles
Visualization of the Kruskal Algorithm
The Kruskal algorithm (or Kruskal's algorithm ) is an efficient algorithm for constructing a minimal spanning tree of a weighted connected non-oriented graph. The algorithm is also used to find some approximations for the Steiner problem [1] . The algorithm was first described by Joseph Kruskal ( Eng. ) In 1956.
Initially, the current set of edges is set to empty. Then, while it is possible, the following operation is carried out: of all the edges, adding them to the already existing set will not cause the cycle to appear in it, selects the edge of the minimum weight and adds it to the already existing set. When there are no more such edges, the algorithm is completed. The subgraph of a given graph containing all its vertices and the set of edges found is its spanning tree of minimum weight. A detailed description of the algorithm can be found in the literature [2] .
Before the algorithm starts, it is necessary to sort the edges by weight, this requires O (E × log (E)) time. After that, it is convenient to store the connected components in the video systems of disjoint sets. All operations in this case will take O (E × α (E, V)) , where α is the function inverse to the Ackermann function. Since for any practical problems α (E, V) <5 , we can take it as a constant, thus, the total time of the Kruskal algorithm can be taken as O (E * log (E)) .
The Kruskal algorithm really finds a spanning tree of minimal weight, since it is a special case of the Rado-Edmonds algorithm. for a graphic matroid, where independent sets are acyclic sets of edges.
| Picture | Description |
|---|---|
 |
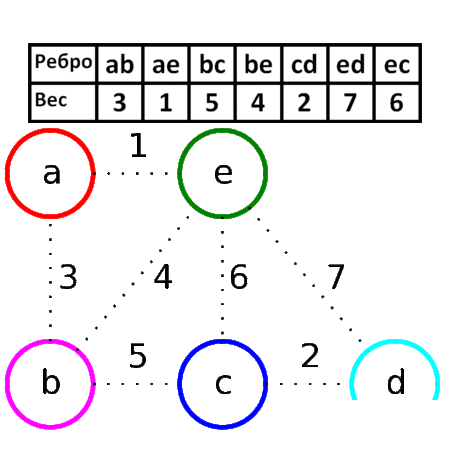
The edges AD and CE have a minimum weight of 5. The edge AD is selected at random (highlighted in the figure). |
 |
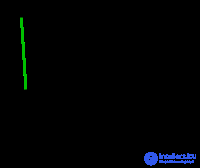
Now the smallest weight, equal to 5, has an edge CE . Since the addition of CE does not form a cycle, we choose it as the second edge. |
 |
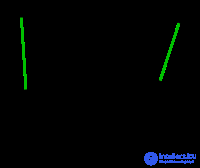
Similarly, choose the edge DF , whose weight is equal to 6. |
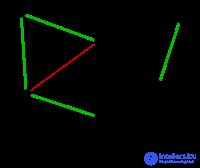 |
The following edges are AB and BE with a weight of 7. Randomly selected edge AB , highlighted in the figure. The edge BD is highlighted in red, since there is already a path (green) between A and D , therefore, if this edge were chosen, an ABD cycle would form. |
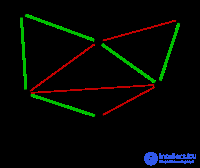 |
Similarly, the BE edge is selected, the weight of which is 7. At this stage, much more edges are highlighted in red: BC , because it creates the BCE cycle, DE , because it creates the DEBA cycle, and FE , because it forms the FEBAD cycle. |
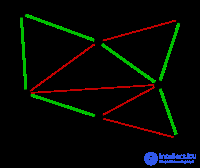 |
The algorithm is completed by adding an EG edge with a weight of 9. A minimum spanning tree has been built. |
Comments
To leave a comment
Algorithms
Terms: Algorithms