Lecture
The theory of algorithms is a branch of computer science that studies the general properties and laws of algorithms and various formal models of their presentation. The problems of the theory of algorithms include formal proof of the algorithmic unsolvability of problems, asymptotic analysis of the complexity of algorithms, classification of algorithms according to complexity classes, development of criteria for comparative evaluation of the quality of algorithms, etc. Together with mathematical logic, the theory of algorithms forms the theoretical basis of computational sciences. [1] [2]
The development of the theory of algorithms begins with the proof by K. Gödel of incompleteness theorems for formal systems including arithmetic, the first of which was proved in 1931. The assumption arising in connection with these theorems about the impossibility of algorithmic resolution of many mathematical problems (in particular, problems of derivability in the predicate calculus ) caused the need for standardization of the concept of the algorithm. The first standardized versions of this concept were developed in the 1930s in the works of A. Turing, A. Church and E. Post. The Turing machine they proposed, the Post machine and the Church's lambda calculus turned out to be equivalent to each other. Based on the work of Gödel, S. Kleene introduced the concept of recursive function, which also turned out to be equivalent to the above.
One of the most successful standardized variants of the algorithm is the concept of a normal algorithm introduced by A. A. Markov. It was developed ten years later by Turing, Post, Church, and Kleene in connection with the proof of the algorithmic undecidability of a number of algebraic problems.
It should be noted also a considerable contribution to the theory of algorithms made by D. Knut, A. Aho and J. Ulman. One of the best works on this topic is the book Algorithms: Construction and Analysis by Thomas H. Corman, Charles I. Leiserson, Ronald L. Rivest, Clifford Stein.
Main articles: Thesis of Church Turing , Turing Machine
Alan Turing suggested (known as the Thesis of Church - Turing) that any algorithm in the intuitive sense of the word can be represented by an equivalent Turing machine. Refining the concept of computability on the basis of the notion of the Turing machine (and other equivalent concepts) opened up possibilities for rigorous proof of the algorithmic unsolvability of various mass problems (that is, problems of finding a single method for solving a certain class of problems whose conditions can vary within certain limits). The simplest example of an algorithmically unsolvable mass problem is the so-called algorithm applicability problem (also called the stop problem). It consists in the following: it is required to find a general method that would allow for an arbitrary Turing machine (given through its program) and an arbitrary initial state of the tape of this machine to determine whether the machine will complete in a finite number of steps, or will continue indefinitely.
During the first decade of the history of the theory of algorithms, unsolvable mass problems were discovered only within this theory itself (this includes the applicability problem described above), as well as within mathematical logic (the problem of deducibility in the classical predicate calculus). Therefore, it was believed that the theory of algorithms is a fringe of mathematics that does not matter for such classical sections as algebra or analysis. The situation changed after A. A. Markov and Л..L. Post in 1947 established the algorithmic unsolvability of the equality problem known in algebra for finitely generated and finitely defined semigroups (the so-called Thue problem). Subsequently, the algorithmic undecidability of many other “purely mathematical” mass problems was established. One of the most famous results in this field is the algorithmic undecidability of the tenth Hilbert problem proved by Yu. V. Matiyasevich.
At present, the theory of algorithms develops mainly in three directions.
Main article: Computational complexity theory
The purpose of the analysis of the complexity of the algorithms is to find the optimal algorithm for solving this problem. As the algorithm's optimality criterion, the complexity of the algorithm is chosen, understood as the number of elementary operations that must be performed to solve the problem using this algorithm. The function of labor is the relation that connects the input data of the algorithm with the number of elementary operations.
The complexity of the algorithms depends differently on the input data. For some algorithms, the workload depends only on the data volume, for other algorithms, on the data values, in some cases, the order of data entry can affect the workload. The complexity of many algorithms may in one way or another depend on all the factors listed above.
One of the simplified types of analysis used in practice is asymptotic analysis of algorithms. The goal of asymptotic analysis is to compare the time and other resources spent by different algorithms designed to solve the same problem, with large amounts of input data. Used in the asymptotic analysis, the evaluation of the complexity function, called the complexity of the algorithm , allows you to determine how quickly the complexity of the algorithm increases with increasing data volume. In the asymptotic analysis of algorithms, the notation used in mathematical asymptotic analysis is used. Below are the main estimates of complexity.
The basic estimate of the complexity function of the algorithm f (n) is the estimate 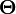 . Here n is the value of the data volume or the length of the input. We say that the estimation of the complexity of the algorithm
. Here n is the value of the data volume or the length of the input. We say that the estimation of the complexity of the algorithm
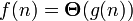
if for g> 0 for n> 0 there are positive ones with 1 , with 2 , n 0 , such that:
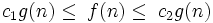
for n> n 0 , in other words, it is possible to find such with 1 and c 2 that for sufficiently large nf (n) will be between
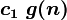 and
and 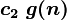 .
.
In this case, it is also said that the function g (n) is an asymptotically exact estimate of the function f (n), since by definition the function f (n) does not differ from the function g (n) up to a constant factor (see asymptotic equality) . For example, for the heapsort sorting method, the evaluation of the laboriousness is
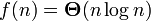 i.e
i.e 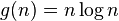
Of 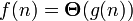 follows that
follows that 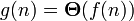 .
.
It is important to understand that 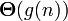 is not a function, but a multitude of functions describing the growth
is not a function, but a multitude of functions describing the growth 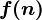 accurate to a constant factor.
accurate to a constant factor.
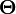 gives simultaneously upper and lower estimates of the growth of the function. It is often necessary to consider these estimates separately. Evaluation
gives simultaneously upper and lower estimates of the growth of the function. It is often necessary to consider these estimates separately. Evaluation 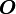 is the upper asymptotic estimate of the complexity of the algorithm. We say that
is the upper asymptotic estimate of the complexity of the algorithm. We say that 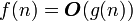 if a
if a
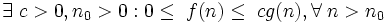
In other words, recording 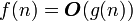 means that f (n) belongs to the class of functions that grow no faster than the function g (n) up to a constant factor.
means that f (n) belongs to the class of functions that grow no faster than the function g (n) up to a constant factor.
Evaluation 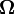 sets the lower asymptotic estimate of the growth of the function f (n) and determines the class of functions that grow no slower than g (n) up to a constant factor.
sets the lower asymptotic estimate of the growth of the function f (n) and determines the class of functions that grow no slower than g (n) up to a constant factor. 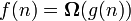 if a
if a
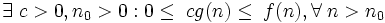
For example, the entry 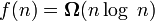 denotes a class of functions that do not grow more slowly than
denotes a class of functions that do not grow more slowly than 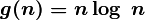 , all polynomials with a degree greater than one fall into this class, as well as all power functions with a base greater than one. Equality
, all polynomials with a degree greater than one fall into this class, as well as all power functions with a base greater than one. Equality 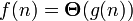 performed if and only if
performed if and only if 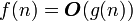 and
and 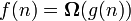 .
.
Asymptotic analysis of algorithms is not only practical, but also theoretical. For example, it was proved that all sorting algorithms based on pairwise comparison of elements will sort n elements in a time no less than 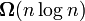 .
.
An important role in the development of asymptotic analysis of algorithms was played by A. Aho, J. Ullman, J. Hopcroft.
Main article: Difficulty class
Within the framework of the classical theory, the classification of problems according to the complexity classes (P-complex, NP-complex, exponentially complex, etc.) is carried out. Class P includes tasks that can be solved in a time that polynomially depends on the volume of the original data using a deterministic computer (for example, a Turing machine), and class NP includes tasks that can be solved in a polynomially pronounced time using a non-deterministic a computer, that is, a machine whose next state is not always uniquely determined by the previous ones. The work of such a machine can be represented as a process branching out at every ambiguity: the problem is considered solved if at least one branch of the process came to the answer. Another definition of the NP class: the NP class includes problems whose solution with the help of additional information of polynomial length given to us from above, we can check in polynomial time. In particular, the class NP includes all problems whose solution can be checked in polynomial time. Class P is contained in class NP. A classic example of an NP problem is the traveling salesman problem.
Since the class P is contained in the class NP, the belonging of one or another task to the class NP often reflects our current understanding of how to solve this problem and is inconclusive. In general, there is no reason to believe that a P-solution cannot be found for a particular NP problem. The question of the possible equivalence of the classes P and NP (that is, the possibility of finding a P-solution for any NP-problem) is considered by many to be one of the main questions of modern complexity theory of algorithms. The answer to this question has not been found so far. The very question about the equivalence of the classes P and NP is possible due to the introduction of the concept of NP-complete problems. NP-complete tasks constitute a subset of NP-problems and are distinguished by the property that all NP-problems can be reduced to them in one way or another. From this it follows that if a P-solution is found for an NP-complete problem, then a P-solution will be found for all problems of class NP. An example of an NP-complete problem is the conjunctive form problem.
Studies of the complexity of algorithms made it possible to take a fresh look at the solution of many classical mathematical problems and to find solutions for a number of such problems (multiplication of polynomials and matrices, solving linear systems of equations, etc.) that require fewer resources than traditional ones.
Comments
To leave a comment
Algorithms
Terms: Algorithms