Lecture
Computational complexity is a concept in computer science and theory of algorithms, denoting a function of the dependence of the amount of work performed by some algorithm on the size of the input data. The section that studies computational complexity is called the theory of computational complexity . The amount of work is usually measured by abstract concepts of time and space, called computational resources. Time is determined by the number of elementary steps needed to solve a problem, while space is determined by the amount of memory or space on the data carrier. Thus, in this area, an attempt is made to answer the central question of algorithm development: “How will the execution time and the amount of memory used change depending on the size of the input?”. Here, the input size is the length of the task data description in bits (for example, in the traveling salesman problem, the input length is almost proportional to the number of cities and roads between them), and the output size is the length of the task solution description (the best route in the traveling salesman problem).
In particular, computational complexity theory defines NP-complete problems that a non-deterministic Turing machine can solve in polynomial time, whereas for a deterministic Turing machine a polynomial algorithm is unknown. These are usually complex optimization problems, for example, the traveling salesman problem.
Such areas as algorithmic analysis and the theory of computability are closely related to theoretical computer science. The connecting link between theoretical informatics and algorithmic analysis is the fact that their formation is devoted to analyzing the required amount of resources of certain algorithms for solving problems, while a more general question is the possibility of using algorithms for such problems. Concretizing, we will try to classify problems that may or may not be solved with the help of limited resources. The strong limitation of available resources distinguishes the theory of computational complexity from the computational theory, the latter answers the question of which tasks can, in principle, be solved algorithmically.
The theory of computational complexity arose from the need to compare the speed of algorithms, clearly describe their behavior (execution time and amount of required memory) depending on the size of the input.
The number of elementary operations spent by the algorithm for solving a particular instance of a problem depends not only on the size of the input data, but also on the data itself. For example, the number of operations of the sorting algorithm by inserts is much smaller in case the input data is already sorted. To avoid such difficulties, consider the concept of temporal complexity of the algorithm in the worst case .
The time complexity of the algorithm (in the worst case) is a function of the size of the input data, equal to the maximum number of elementary operations performed by the algorithm to solve an instance of a problem of the specified size.
Similarly, the concept of temporal complexity in the worst case is determined by the concept of temporal complexity of the algorithm in the best case . Also consider the concept of the average time of the algorithm , that is, the expectation of the time of the algorithm. Sometimes they say simply: “The time complexity of the algorithm ” or “ The running time of the algorithm ”, meaning the time complexity of the algorithm in the worst, best or average case (depending on the context).
By analogy with the temporal complexity, they determine the spatial complexity of the algorithm , only here they speak not about the number of elementary operations, but about the amount of memory used.
Despite the fact that the function of the time complexity of the algorithm in some cases can be determined exactly, in most cases it is pointless to look for its exact value. The fact is that, firstly, the exact value of the time complexity depends on the definition of elementary operations (for example, complexity can be measured in the number of arithmetic operations, bit operations or operations on a Turing machine), and secondly, as the input data size increases multipliers and lower order terms appearing in the expression for exact time of operation become extremely insignificant.
Consideration of large input data and an estimate of the order of growth of the algorithm’s working time lead to the notion of asymptotic algorithm complexity . In this case, an algorithm with a smaller asymptotic complexity is more efficient for all input data, with the exception of only, possibly, small data. Asymptotic notation is used to record the asymptotic complexity of algorithms:
| Designation | Intuitive explanation | Definition |
|---|---|---|
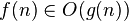 |  bounded above by function bounded above by function  (accurate to a constant factor) asymptotically (accurate to a constant factor) asymptotically | 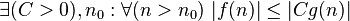 or or 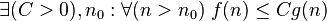 |
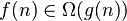 |  limited to bottom function limited to bottom function  (accurate to a constant factor) asymptotically (accurate to a constant factor) asymptotically | 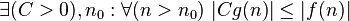 |
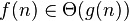 |  bounded above and below by function bounded above and below by function  asymptotically asymptotically | 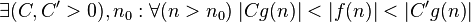 |
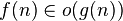 |  dominates dominates  asymptotically asymptotically | 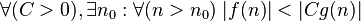 |
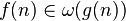 |  dominates dominates  asymptotically asymptotically | 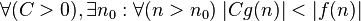 |
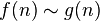 |  is equivalent to is equivalent to  asymptotically asymptotically | 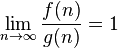 |
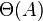 ), that is, on a carpet whose area is more than twice, it will take twice as long. Accordingly, with an increase in the area of the carpet a hundred thousand times, the amount of work increases strictly proportionally one hundred thousand times, and so on.
), that is, on a carpet whose area is more than twice, it will take twice as long. Accordingly, with an increase in the area of the carpet a hundred thousand times, the amount of work increases strictly proportionally one hundred thousand times, and so on. 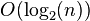 ), since opening the book approximately in the middle, we reduce the size of the “remaining problem” by half (by sorting the names alphabetically). Thus, in a book 1000 pages thick, any name is no more than
), since opening the book approximately in the middle, we reduce the size of the “remaining problem” by half (by sorting the names alphabetically). Thus, in a book 1000 pages thick, any name is no more than 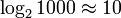 times (book openings). By increasing the page size to one hundred thousand, the problem is still solved in
times (book openings). By increasing the page size to one hundred thousand, the problem is still solved in 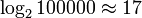 of visits. (See Binary Search.)
of visits. (See Binary Search.) Insofar as 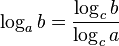 , in the asymptotic estimate of complexity it is often written “logarithm” without mentioning the base - for example,
, in the asymptotic estimate of complexity it is often written “logarithm” without mentioning the base - for example, 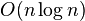 .
.
It must be emphasized that the growth rate of the worst execution time is not the only or the most important criterion for evaluating algorithms and programs. Here are a few considerations that allow us to look at the run-time criterion from other points of view:
If the created program is used only a few times, then the cost of writing and debugging the program will dominate the total cost of the program, that is, the actual execution time will not have a significant impact on the total cost. In this case, you should prefer the algorithm that is the easiest to implement.
If the program will work only with “small” input data, the degree of growth in the execution time will be less important than the constant present in the execution time formula [1] . At the same time, the concept of “smallness” of input data depends on the exact execution time of competing algorithms. There are algorithms, such as the algorithm of integer multiplication, which are asymptotically the most effective, but which are never used in practice even for large tasks, since their proportionality constants far exceed those of other, simpler and less “efficient” algorithms. Another example is the Fibonacci heaps, despite the asymptotic efficiency, from a practical point of view, the software implementation complexity and the large values of the constants in the work time formulas make them less attractive than ordinary binary trees [1] .
 | If the solution of a problem for an n-vertex graph with one algorithm takes time (number of steps) of order n C , and with the other, takes n + n! / C, where C is a constant number, then according to the “polynomial ideology” the first algorithm is practically effective , and the second is not, although, for example, at C = 10 (10 10 ), the situation is just the opposite. [2] A. A. Zykov |  |
Efficient, but complex algorithms may be undesirable if ready-made programs are supported by persons not involved in writing these programs.
There are examples when effective algorithms require such large amounts of computer memory (without the possibility of using slower external storage media) that this factor negates the advantage of the algorithm. Thus, it is often important not only “time complexity”, but also “memory complexity” (spatial complexity).
In numerical algorithms, the accuracy and stability of algorithms are no less important than their temporal efficiency.
The complexity class is a set of recognition tasks, for the solution of which there are algorithms that are similar in computational complexity. Two important representatives:
The class P contains all those problems whose solution is considered “fast”, that is, the solution time of which depends polynomially on the size of the input. This includes sorting, searching in a set, finding out whether graphs are connected, and many others.
The NP class contains tasks that a non-deterministic Turing machine is able to solve in a polynomial number of steps of the size of the input data. It should be noted that the non-deterministic Turing machine is only an abstract model, while modern computers correspond to the deterministic Turing machine with limited memory. Since a deterministic Turing machine can be considered as a special random deterministic Turing machine, class NP includes class P, as well as some problems for which only algorithms are known that are exponentially dependent on the size of the input (that is, ineffective for large inputs). The NP class includes many famous problems, such as the traveling salesman problem, the problem of satisfiability of Boolean formulas, factorization, etc.
The question of the equality of these two classes is considered one of the most difficult open problems in the field of theoretical informatics. The Clay Institute of Mathematics included this problem in the list of problems of the millennium, by offering a reward of one million US dollars for its solution.
Comments
To leave a comment
Algorithms
Terms: Algorithms