Lecture

4 vertex tournament
tops 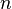
ribs: 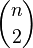
A tournament is a directed graph obtained from an undirected full graph by assigning a direction to each edge. Thus, a tournament is a digraph in which each pair of vertices is connected by one directed arc.
Many important tournament features have been reviewed by Landau [1] in order to investigate the chick dominance model in the flock. Current tournaments applications include research in the field of voting and collective choice among other things. The name of the tournament comes from the graphical interpretation of the outcomes of a round-robin tournament, in which each player meets each other player exactly once, and in which there can be no draws. In the tournament digraph, the tops correspond to the players. The arc between each pair of players is oriented from the winner to the loser. If a player  wins the player
wins the player 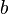 then say that
then say that  dominates
dominates 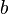 .
.
Any tournament with a finite number 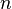 vertices contains a Hamiltonian path, that is, an oriented path containing all
vertices contains a Hamiltonian path, that is, an oriented path containing all 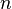 vertices [2] . This is easily shown by mathematical induction on
vertices [2] . This is easily shown by mathematical induction on 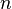 : let the statement be true for
: let the statement be true for 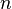 and let there be some tournament
and let there be some tournament 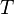 with
with 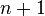 tops. Pick vertex
tops. Pick vertex 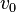 at
at 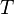 let it go
let it go 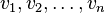 - directional path to
- directional path to 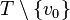 . Let be
. Let be 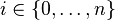 - the maximum number, such that for any
- the maximum number, such that for any  there is an arc of
there is an arc of 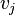 at
at 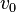 . Way
. Way

- the desired oriented path. This proof also provides the search algorithm for the Hamiltonian path. Known more efficient algorithm that requires iteration of all 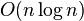 arcs [3] .
arcs [3] .
This means that a strictly connected tournament has a Hamiltonian cycle [4] . More strictly: any strongly connected tournament is vertex-pancyclic [en] - for any vertex v and for any k from three to the number of vertices in the tournament there is a cycle of length k containing v . [5] . Moreover, if a tournament is 4-connected, any pair of vertices can be connected by the Hamiltonian path [6] .

Transitive tournament with 8 vertices.
Tournament in which 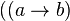 and
and 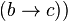
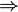
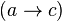 is called transitive . In a transitive tournament, tops can be completely ordered in order of reachability.
is called transitive . In a transitive tournament, tops can be completely ordered in order of reachability.
The following statements for a tournament with n vertices are equivalent:
Transitive tournaments play a significant role in Ramsey theory, similar to the role played by clicks in undirected graphs. In particular, any tournament with n vertices contains a transitive sub-tournament with 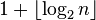 tops. [7] The proof is simple: choose any vertex v as a part of this subtournament and construct a subtournament recursively on the set of either the incoming neighbors of the vertex v or the set of outgoing neighbors, depending on which set is larger. For example, any tournament with seven peaks contains a transitive tournament with three peaks. The seven-top Paley Tournament shows that this is the maximum that can be guaranteed [7] . However, Reid and Parker [8] showed that this boundary is not strict for some large values of the number n .
tops. [7] The proof is simple: choose any vertex v as a part of this subtournament and construct a subtournament recursively on the set of either the incoming neighbors of the vertex v or the set of outgoing neighbors, depending on which set is larger. For example, any tournament with seven peaks contains a transitive tournament with three peaks. The seven-top Paley Tournament shows that this is the maximum that can be guaranteed [7] . However, Reid and Parker [8] showed that this boundary is not strict for some large values of the number n .
Erdos and Moser [7] proved that there are tournaments with n vertices without transitive size sub-tournaments. 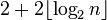 . Their proof uses counting [en] : the number of variants in which a transitive tournament with k vertices can be contained in a larger tournament with n marked vertices is equal to
. Their proof uses counting [en] : the number of variants in which a transitive tournament with k vertices can be contained in a larger tournament with n marked vertices is equal to
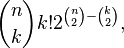
and with k superior 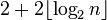 this number is too small for a transitive tournament to be in each of
this number is too small for a transitive tournament to be in each of 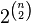 different tournaments of the same set of n marked vertices.
different tournaments of the same set of n marked vertices.
The player who wins all the games will naturally be the winner of the tournament. However, as the existence of nontransitive tournaments shows, such a player may not be. A tournament in which each player loses at least one game is called a 1-paradoxical tournament. Generally, a Tournament T = ( V , E ) is called k- paradoxical, if for any k -element subset S of V there is a vertex v 0 in 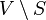 such that
such that 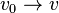 for all
for all 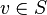 . Using the probabilistic method [ru], Erdёs showed that for any fixed k subject to | V | ≥ k 2 2 k ln (2 + o (1)) almost any tournament on V is k- paradoxical. [9] On the other hand, a simple argument shows that any k- paradoxical tournament must have at least 2 k +1 - 1 players, which has been improved to ( k + 2) 2 k −1 - 1 Esther and Györgye Sekresres ( 1965) [10] . There is an explicit method for constructing k- paradoxical tournaments with k 2 4 k −1 (1 + o (1)) players, developed by Graham and Spencer, namely, Paley's tournament [11] .
. Using the probabilistic method [ru], Erdёs showed that for any fixed k subject to | V | ≥ k 2 2 k ln (2 + o (1)) almost any tournament on V is k- paradoxical. [9] On the other hand, a simple argument shows that any k- paradoxical tournament must have at least 2 k +1 - 1 players, which has been improved to ( k + 2) 2 k −1 - 1 Esther and Györgye Sekresres ( 1965) [10] . There is an explicit method for constructing k- paradoxical tournaments with k 2 4 k −1 (1 + o (1)) players, developed by Graham and Spencer, namely, Paley's tournament [11] .
Condensation [en] of any tournament is a transitive tournament. Thus, even if a tournament is not transitive, the strongly related components of a tournament can be completely streamlined. [12]
The sequence of a tournament score is a non-decreasing sequence of half-degrees of the outcome of the tournament tops. The tournament score set is the set of integers that are semi-degrees of the outcome of the tournament tops.
Landau's theorem (1953) Non-decreasing sequence of integers 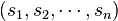 is a counting sequence if and only if:
is a counting sequence if and only if:
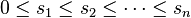
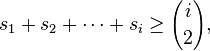 for
for 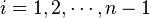
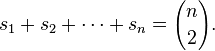
Let be  - number of different size counting sequences
- number of different size counting sequences 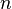 . Sequence
. Sequence 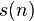 begin with:
begin with:
1, 1, 1, 2, 4, 9, 22, 59, 167, 490, 1486, 4639, 14805, 48107, ...
(sequence A000571 in OEIS)
Winston and Kleitman proved that for sufficiently large n
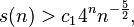
Where 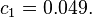 Takacs later showed [13] using some plausible but unproved assumption that
Takacs later showed [13] using some plausible but unproved assumption that

Where 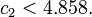
Together, this suggests that
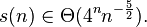
Here  reflects the asymptotically strict boundary.
reflects the asymptotically strict boundary.
Yao showed [14] that any non-empty set of non-negative integers is a score set for some tournament.
Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.