Lecture
A matroid is a classification of subsets of a certain set, which is a generalization of the idea of independence of elements, analogous to the independence of elements of a linear space, into an arbitrary set.
Matroid - a pair 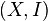 where
where 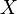 - a finite set, called a matroid carrier, and
- a finite set, called a matroid carrier, and 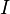 - some set of subsets
- some set of subsets 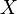 called the family of independent sets, i.e.
called the family of independent sets, i.e. 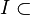
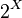 . The following conditions must be met:
. The following conditions must be met:
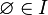
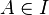 and
and 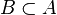 then
then 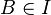
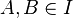 and power A is more power B, then there is
and power A is more power B, then there is 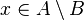 such that
such that 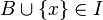
The bases of the matroid are the maximal independent sets with respect to inclusion. Subsets 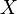 not owned
not owned 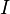 are called dependent sets. The minimal inclusion sets of dependent sets are called matroid cycles , this concept is used in the alternative definition of a matroid.
are called dependent sets. The minimal inclusion sets of dependent sets are called matroid cycles , this concept is used in the alternative definition of a matroid.
Matroid - a pair 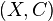 where
where 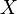 - carrier matroid, and
- carrier matroid, and 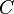 - family of non-empty subsets
- family of non-empty subsets 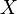 , called the set of matroid cycles for which the following conditions are true: [1]
, called the set of matroid cycles for which the following conditions are true: [1]
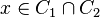 then
then 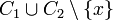 contains a loop
contains a loop Let be 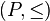 - partially ordered set.
- partially ordered set.  - short circuit in
- short circuit in 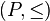 , if a
, if a
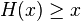
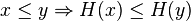
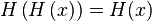
Will consider 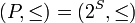 the case when a partially ordered set is a Boolean algebra. Let be
the case when a partially ordered set is a Boolean algebra. Let be 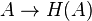 - closure
- closure 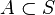 .
.
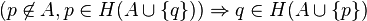
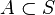 there is such
there is such 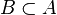 , what
, what 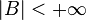

Couple  where
where 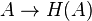 - correct circuit to
- correct circuit to 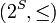 is called a matroid .
is called a matroid .
We define the set E as a set consisting of {1, 2, 3, .., n} - numbers of columns of a certain matrix, and the set I, as a set consisting of subsets of E, such that the vectors determined by them are linearly independent over the field real numbers R. Let us ask ourselves the question - what properties does the constructed set I have?
We will prove that in the considered example the set of linearly independent columns is indeed a matroid. To do this, it suffices to prove the third property from the definition of a matroid. We carry out the proof by contradiction.
Evidence. Let A, B ∈ I and | A | = | B | + 1. Let W be the space of vectors spanned by A ∪ B. It is clear that its dimension will be at least | A |. Suppose that B ∪ {x} will be linearly dependent for all x ∈ A - B (that is, the third property will not hold). Then B forms a basis in the space W. From this it follows that | A | ≤ dim W ≤ | B |. But since, by assumption, A and B consist of linearly independent vectors and | A | > | B |, we obtain a contradiction. Such a set of vectors will be a matroid.

Matroids with a small number of elements are often depicted as diagrams. Points are elements of the main set, and curves are “stretched” through each three-element chain (3-element circuit). The diagram shows a 3-rank matroid, called Fano's matroid, an example that appeared in a 1935 article in Whitney.
The name comes from the fact that the Fano matroid is a second-order projective plane, known as the Fano plane, whose coordinate field is a two-element field. This means that Fano's matroid is a vector matroid associated with seven non-zero vectors in a three-dimensional vector space above the field of two elements.
It is known from projective geometry that a Froid matroid is not representable by an arbitrary set of vectors in a real or complex vector space (or in any vector space over a field whose characteristics differ from 2).
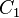 and
and 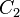 - cycles, then for any
- cycles, then for any 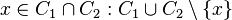 contains a loop
contains a loop 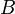 - base and
- base and 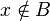 then
then 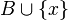 contains exactly one cycle.
contains exactly one cycle. http://rain.ifmo.ru/cat/view.php/theory/unsorted/matroids-2004/
Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.