Set

Set is one of the key concepts of mathematics, in particular, set theory and logic.

The concept of a set is usually taken as one of the original (axiomatic) concepts, that is, irreducible to other concepts, and therefore not having a definition; descriptive formulations are used to explain it, characterizing the set as a set of different elements, conceivable as a whole ^{[1] [2]} . Indirect definition is also possible through axioms of set theory. A set can be empty and non-empty, ordered and unordered, finite and infinite, an infinite set can be countable or uncountable. Moreover, in both naive and axiomatic set theories, any object is usually considered a set.

The history of the concept

The foundations of the theory of finite and infinite sets were laid by Bernard Bolzano, who formulated some of its principles.

From 1872 to 1897 (mainly in 1872–1884), Georg Cantor published a series of papers in which the main sections of set theory were systematically described, including the theory of point sets and the theory of transfinite numbers (cardinal and ordinal). In these works, he not only introduced the basic concepts of set theory, but also enriched mathematics with new type of reasoning, which he applied to prove theorems of set theory, in particular, for the first time to infinite sets. Therefore, it is generally accepted that Georg Cantor created set theory. In particular, he defined the set as “a single name for the totality of all objects with this property”. These objects are called elements of the set. Many objects with property 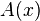outlined 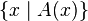. If some set 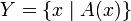then 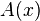called the characteristic property of the set .

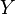This concept led to paradoxes, in particular, to the Russell paradox.

Since set theory is actually used as the basis and language of all modern mathematical theories in 1908, set theory was axiomatized independently by Bertrand Russell and Ernst Zermelo. In the future, many researchers have revised and modified both systems, mostly retaining their character. Until now, they are still known as the Russell Type Theory and Zermelo Set Theory. Subsequently, the theory of sets of Kantor was called the naive theory of sets, and the newly constructed theory - the axiomatic theory of sets.

In the practice that has developed since the middle of the XX century, the set is defined as a model that satisfies the ZFC axioms (Zermelo – Fraenkel axioms with the axiom of choice). With this approach, in some mathematical theories arise sets of objects that are not sets. Such aggregates are called classes (of various orders).

Element set

The objects that make up a set are called the elements of a set or points of a set. Sets are most often denoted by capital letters of the Latin alphabet, its elements - lowercase. If a 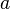- set element 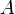then write down 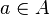(" 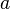belongs 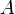"). If a 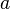not an element of the set 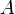then write down 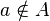(" 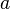not belong 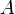"). Unlike a multiset, each element of a set is unique, and there cannot be two identical elements in a set. In other words, adding to the set of elements identical to those already belonging to the set does not change it:

.

Some kinds of sets and similar objects

Special sets

• An empty set is a set that does not contain a single element.
• A universal set (universe) is a set containing all conceivable objects. In connection with the Russell paradox, this concept is currently interpreted as “a set that includes all the sets participating in the problem under consideration”.
• A partially ordered set, a completely ordered set — a set on which an order relation is given.

Related Objects

• A tuple (in particular, an ordered pair) is an ordered set of a finite number of named objects. It is recorded inside parentheses or angle brackets, and elements can be repeated.
• A multiset (in the theory of Petri nets is called “set”) is a set with multiple elements.
• A space is a set with some additional structure.
• A vector is an element of a linear space containing a finite number of elements of some field as coordinates. The order matters, the elements can be repeated.
• The sequence is a function of one natural variable. It is represented as an infinite set of elements (not necessarily different), the order of which matters.
• A fuzzy set is a mathematical object that is similar to a set whose membership is defined not by a relation, but by a function. In other words, with respect to the elements of a fuzzy set, one can say “to what extent” they are included in it, and not just whether they are included in it or not.

By hierarchy

• The set of sets (in particular, a boolean is the set of all subsets of a given set).
• Subset
• Superset

Relationships between sets

Venn diagram for

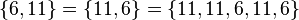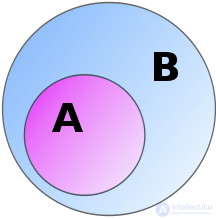
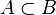
Two sets 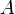and 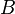may enter into different relationships with each other.

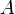• included in 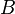if each element of the set 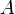also belongs to the set :

  

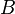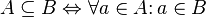
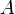• includes 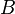, if a 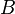included in :

  

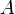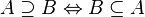
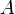• equally 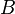, if a 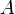and 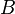included in each other:

  

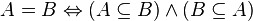
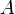• strictly included in 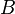, if a 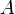included in 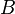but not equal to him:

  

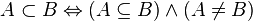
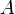• strictly includes 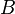, if a 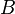strictly included in :

  

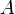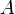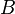• and do not intersect if they have no common elements:

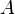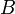  and do not intersect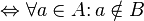

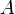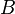• and are in general position if there exists an element belonging exclusively to the set 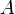, an element belonging exclusively to the set 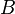, as well as an element belonging to both sets:

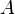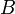  and are in general position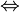

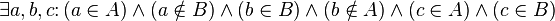
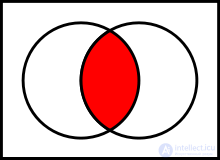
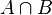
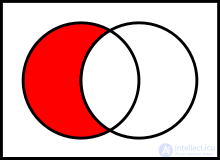
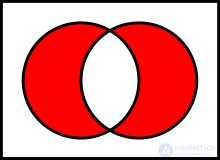
Set Operations

Venn diagram for

Venn diagram for

Venn diagram for

Venn diagram for

Binary operations

Basic binary operations defined on sets:

• intersection:

  .

• Union:

  .

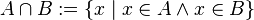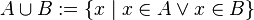If sets 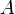and 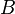don't intersect then 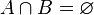. Their association also means: .

• difference:

  .

• symmetric difference:

  .

• Cartesian or direct product:

  .

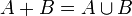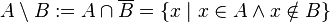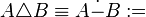
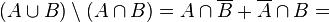
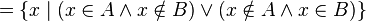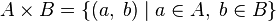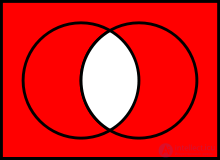
To explain the meaning of operations, Venn diagrams are often used, which present the results of operations on geometric shapes as sets of points.

Any system of sets that is closed with respect to the operations of union and intersection forms a distributive lattice with respect to the union and intersection.

Unary operations

Venn diagram for

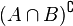
Addition is determined as follows:

.

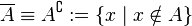The addition operation implies some fixed universe (the universal set 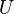which contains 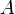), and it comes down to the difference of sets with this universe:

.

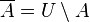The system of sets with a fixed universe, closed with respect to the operations of union, the intersection with the addition thus introduced forms a Boolean algebra.

Boolean - the set of all subsets:

.

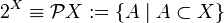Designation 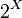derives from the power property of the set of all subsets of a finite set:

.

Boolean 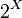generates a system of sets with a fixed universe 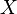, closed with respect to the operations of union and intersection, that is, forms a Boolean algebra.

Priority operations

First, unary operations (additions) are performed, then intersections, then unions and differences that have the same priority. The sequence of operations can be changed by brackets.

Power

The power of a set is a characteristic of a set that generalizes the concept of the number of elements for a finite set in such a way that sets between which it is possible to establish a bijection are equal. Denoted by 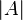or 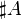. The power of an empty set is zero; for finite sets, the power coincides with the number of elements; for infinite sets, special cardinal numbers are introduced that correspond with each other according to the inclusion principle (if 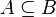then 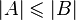) and the propagation of the power property of a boolean of a finite set: 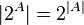in the case of infinite sets (the very notation 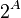motivated by this property).

The smallest infinite power is indicated by 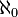This is the power of a countable set. The power of the continuum, a bijective boolean of a countable set, is denoted by or 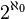. Continuum hypothesis is the assumption that there are no intermediate powers between the calculated power and the power of the continuum.

Notes