Lecture

The Hamiltonian line for the dodecahedron proposed by Hamilton to replace his “around the world” game on the dodecahedron with a problem for a planar graph.
Hamiltonian graph is a mathematical object of graph theory. It is a graph (a set of points and lines connecting them), which contains the Hamiltonian cycle [1] . In this case, the Hamiltonian cycle is such a cycle (closed path), which contains all the vertices (points) of this graph [2] .
Also, the concept of the Hamiltonian path is closely related to the Hamilton graph, which is a simple path (a path without loops) that passes through each vertex of the graph exactly once [1] . Hamiltonian path differs from the cycle in that the path of the start and end points may not coincide, unlike the cycle. The Hamiltonian cycle is the Hamiltonian path.
The Hamiltonian path, cycle and graph are named after the Irish mathematician W. Hamilton, who first defined these classes by examining the “round-the-world travel” task of the dodecahedron. In this task, the tops of the dodecahedron symbolized famous cities, such as Brussels, Canton, Delhi, Frankfurt, etc., and the edges - the roads connecting them. The traveler must pass "around the world", finding a path that passes through all the peaks exactly once [3] . To make the task more interesting, the order of passing cities was established in advance. And to make it easier to remember which cities are already connected, a nail was hammered into each vertex of the dodecahedron, and the paved path was marked with a small rope that could be wrapped around the nail. However, this construction was too cumbersome, and Hamilton proposed a new version of the game, replacing the dodecahedron with a flat graph isomorphic to the graph built on the edges of the dodecahedron [4] .
A necessary condition for the existence of a Hamiltonian path in an undirected graph : if an undirected graph G contains a Hamiltonian cycle, then there is not a single vertex in it  with a local degree
with a local degree 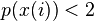 . The proof follows from the definition.
. The proof follows from the definition.
Posha condition: Let graph G have  vertices. If for everyone
vertices. If for everyone 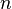 ,
, 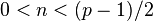 , the number of vertices with powers greater than or equal to n is less than n, and for odd
, the number of vertices with powers greater than or equal to n is less than n, and for odd  number of vertices with degree
number of vertices with degree 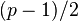 does not exceed
does not exceed 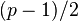 , then G is a Hamiltonian graph. This sufficient condition is not necessary [5] .
, then G is a Hamiltonian graph. This sufficient condition is not necessary [5] .
As a consequence of the Posch theorem, we obtain simpler and less strong sufficient conditions found by Dirac and Ore.
In 1952, the Dirac condition of the existence of the Hamiltonian path was formulated:  - the number of vertices in this graph and
- the number of vertices in this graph and 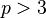 ; if the degree of each vertex is not less than
; if the degree of each vertex is not less than 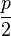 then this graph is Hamiltonian [6] .
then this graph is Hamiltonian [6] .
Main article: Ore Theorem
Ore condition : let  - the number of vertices in the graph and
- the number of vertices in the graph and  . If for any pair of nonadjacent vertices
. If for any pair of nonadjacent vertices  inequality fulfilled
inequality fulfilled  then this graph is Hamiltonian (in other words: the sum of the degrees of any two non-adjacent vertices is not less than the total number of vertices in the graph) [6] .
then this graph is Hamiltonian (in other words: the sum of the degrees of any two non-adjacent vertices is not less than the total number of vertices in the graph) [6] .
The Bondi-Hvatala theorem summarizes the statements of Dirac and Ore. For a graph G with n vertices, the closure is determined by adding an edge ( u , v ) to G for each pair of non-adjacent vertices u and v whose sum of degrees is at least n [7] (in other words: a graph is Hamiltonian if and only if its closure - Hamilton graph).
With a direct enumeration of vertex variants, it is possible to significantly increase the average complexity of finding the Hamiltonian path on random graphs (if the Hamiltonian path in the graph is guaranteed). To improve this method, it is possible at each iteration step with a certain part of the chain to check whether the remaining vertices form a connected graph (if they do not form, then the chain cannot be the beginning of the Hamiltonian chain); at each step of the search, when selecting the next vertex, try first the vertices with the lowest residual degree (the number of edges leading to the not yet visited vertices). In addition, if this tree is a chain, then a Hamiltonian cycle is possible in it. Otherwise (if there are vertices in the tree with degree not less than 3) the construction of the Hamiltonian cycle is impossible.
Hamiltonian cycle is used in the system of so-called protocols with zero resolution .
Let Marc and Vadim know the same Hamiltonian graph G, and Marc knows the Hamiltonian cycle in it. He wants to prove it to Vadim, without revealing to him the cycle itself. There is an algorithm for how it should act [8] :
1. Mark randomly transforms the graph G. Moving the points and changing their labels, he creates a new graph H, topologically isomorphic to G. Then, knowing the Hamiltonian cycle in G, he will easily find it in H. If he does not create H himself, then the definition isomorphism between graphs is too difficult task, the solution of which requires a huge amount of time. He then encrypts H and gets the graph H / .
2. Mark transmits to Vadim H / .
3. Vadim asks Mark either:
4. Mark fulfills his request. He either:
5. Mark and Vadim repeat steps 1 - 4 n times.
If Mark is not deceiving, then he will be able to tell Vadim one of the evidence in step 3. However, if he does not know the Hamiltonian cycle for G, he will not be able to create H / satisfying both proofs. True, Mark can create either a graph isomorphic to G, or a graph with the same number of vertices and edges and a regular Hamiltonian cycle. And, although with a probability of 50% he can guess what evidence Vadim asks at stage 3, Vadim can repeat the protocol a sufficient number of times until he is convinced that Mark knows the Hamiltonian cycle in G.
A salesman needs to visit each city within a certain territory and return to the point of departure. It is required that the path be as short as possible. Thus, the original task is transformed into the task of finding the minimum length (duration or cost) [9] .
The task can be reformed in terms of graph theory - to construct such a graph G (X, A), the vertices of which correspond to cities, and the edges to communications between cities. The solution to this problem is sought among the Hamiltonian cycles of the constructed graph.
There are many ways to solve this problem. We can distinguish methods developed by Bellmore and Nemhauser [10] , Garfinkel and Nemhauser [11] , Held and Karp [12] , and Stekhan [13] . Also known solutions of the traveling salesman problem are the branch and bound method and the method of sequential improvement of the solution [14] .

Hamilton dedicated loop dodecahedron graph
A semi-Hamiltonian [15] graph is a graph containing a simple chain passing through each of its vertices. Moreover, every Hamiltonian graph is semi-Hamiltonian. The Hamiltonian cycle is a simple spanning cycle [16] .
The essence of the Hamiltonian cycle problem is to find out whether the given graph G has Hamiltonian cycle. This task is an NP-complete [17] .
The Hamiltonian orchain of the digraph [18] is a simple chain that passes through each vertex of the digraph exactly once.
The Hamiltonian orcyc [18] is called the ortsikl [18] of the digraph that passes through each of its vertices, is called .
An orgraph is called semi-Hamiltonian [18] if it has a Hamiltonian orchain, and a Hamiltonian [18] if it has a Hamiltonian orcyclic ring.
Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.