Lecture
Binary relation in mathematics is a two-place relationship between any two sets 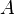 and
and 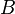 , that is, every subset of the Cartesian product of these sets:
, that is, every subset of the Cartesian product of these sets: 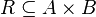 [1] . Binary relation on set
[1] . Binary relation on set 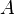 - any subset
- any subset 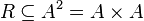 Such binary relations are most often used in mathematics, in particular, such are equality, inequality, equivalence, order relation.
Such binary relations are most often used in mathematics, in particular, such are equality, inequality, equivalence, order relation.
The set of all the first elements of pairs from 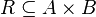 called the domain definition area
called the domain definition area  and is denoted as
and is denoted as  .
.
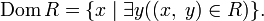
 is called a relationship value area
is called a relationship value area  and is denoted by
and is denoted by 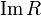 .
.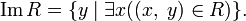
 - it's a lot
- it's a lot 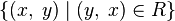 and is denoted as
and is denoted as 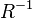 .
. and
and 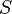 - it's a lot
- it's a lot  and is denoted as
and is denoted as 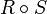 .
.Binary relation  on some set
on some set 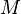 may have different properties, for example:
may have different properties, for example:
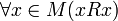 ,
,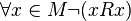 ,
,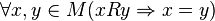 ,
,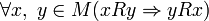 ,
,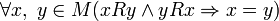 ,
,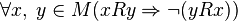 is equivalent to the simultaneous anti-reflexivity and antisymmetry of the relationship,
is equivalent to the simultaneous anti-reflexivity and antisymmetry of the relationship,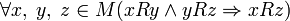 ,
,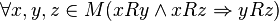 ,
, ,
,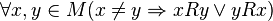 ,
,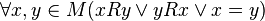 ,
,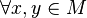 exactly one of three statements is true:
exactly one of three statements is true: 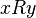 ,
, 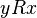 or
or 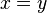 .
.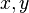 performed
performed 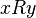 or
or 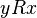 a) transitive relation is called a linear order relation.
a) transitive relation is called a linear order relation. ) - is a double ratio consisting of pairs of elements
) - is a double ratio consisting of pairs of elements 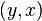 obtained by rearranging pairs of elements
obtained by rearranging pairs of elements 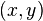 this relationship
this relationship  . Denoted by:
. Denoted by: 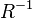 . For a given relation and its inverse, the equality is true:
. For a given relation and its inverse, the equality is true: 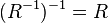 .
. defined on some set and characterized in that for any
defined on some set and characterized in that for any 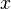 of this set element
of this set element 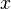 is in relation
is in relation  to oneself that is for any element
to oneself that is for any element 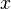 of this set takes place
of this set takes place 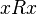 . Examples of reflexive relations: equality, simultaneity, similarity.
. Examples of reflexive relations: equality, simultaneity, similarity. defined on some set and characterized in that for any element
defined on some set and characterized in that for any element 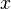 this set is incorrect that it is in relation
this set is incorrect that it is in relation  to myself (wrong that
to myself (wrong that 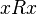 ), that is, it is possible that the element of the set is not in relation
), that is, it is possible that the element of the set is not in relation  to myself.
to myself. defined on some set and characterized by the fact that for any
defined on some set and characterized by the fact that for any  of
of 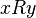 and
and 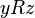 follows
follows 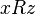 (
( 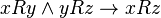 ). Examples of transitive relations: “more”, “less”, “equal”, “like”, “higher”, “north”.
). Examples of transitive relations: “more”, “less”, “equal”, “like”, “higher”, “north”. defined on some set and characterized by the fact that for any
defined on some set and characterized by the fact that for any  of this set of
of this set of 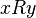 and
and 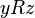 it does not follow
it does not follow 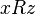 (
( 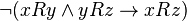 ). An example of a non-transitive relationship: “x father y”
). An example of a non-transitive relationship: “x father y” defined on some set and characterized in that for any elements
defined on some set and characterized in that for any elements 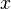 and
and 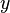 of this set of what
of this set of what 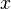 is to
is to 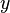 in a relationship
in a relationship  follows that and
follows that and 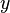 is in the same attitude
is in the same attitude 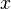 -
- 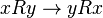 . An example of symmetric relations can be equality, equivalence relation, similarity, simultaneity.
. An example of symmetric relations can be equality, equivalence relation, similarity, simultaneity. defined on some set and characterized by the fact that for any
defined on some set and characterized by the fact that for any 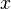 and
and 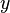 of
of 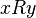 and
and 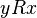 follows
follows 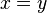 (i.e
(i.e  and
and 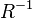 performed at the same time only for equal members).
performed at the same time only for equal members). defined on some set and characterized by the fact that for any
defined on some set and characterized by the fact that for any 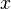 and
and 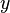 of
of 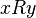 follows
follows 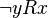 . Example: the relationship “more” (>) and “less” (<).
. Example: the relationship “more” (>) and “less” (<). between objects
between objects 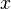 and
and 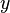 which is both reflexive, symmetric and transitive. Examples: equality, equal power of two sets, similarity, simultaneity.
which is both reflexive, symmetric and transitive. Examples: equality, equal power of two sets, similarity, simultaneity. defined on some set, characterized in that each value
defined on some set, characterized in that each value 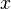 relations
relations 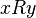 only a single value matches
only a single value matches 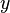 . Relationship Feature Property
. Relationship Feature Property  written in the form of an axiom:
written in the form of an axiom: 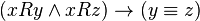 .
. defined on some set, characterized by the fact that it has every value
defined on some set, characterized by the fact that it has every value 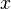 matches a single value
matches a single value 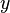 and each value
and each value 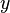 matches a single value
matches a single value 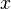 .
. defined on some set, characterized in that for any two different elements
defined on some set, characterized in that for any two different elements 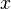 and
and 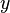 of this set, one of them is in relation
of this set, one of them is in relation  to the other (that is, one of the two relations is satisfied:
to the other (that is, one of the two relations is satisfied: 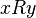 or
or 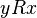 ). Example: “less than” ratio (<).
). Example: “less than” ratio (<).Since the relations defined on a fixed pair of sets 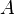 and
and 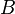 the essence of a subset of a set
the essence of a subset of a set 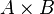 , then the totality of all these relations forms a Boolean algebra with respect to the operations of uniting, intersecting, and complementing relations. In particular, for arbitrary
, then the totality of all these relations forms a Boolean algebra with respect to the operations of uniting, intersecting, and complementing relations. In particular, for arbitrary 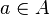 ,
, 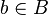 :
:
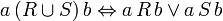 ,
,
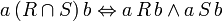 ,
,
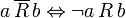 .
.
Often, instead of combining, intersecting and complementing relationships, they talk about their disjunction, conjunction, and denial.
For example, 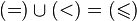 ,
, 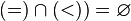 , that is, the union of a strict order relation with an equality relation coincides with a nonstrict order relation, and their intersection is empty.
, that is, the union of a strict order relation with an equality relation coincides with a nonstrict order relation, and their intersection is empty.
In addition to the above, the operations of inversion and multiplication of relations, defined as follows, are important. If a 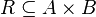 , the inverse relation is called the relation
, the inverse relation is called the relation 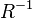 determined on pair
determined on pair 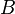 ,
, 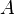 and consisting of those pairs
and consisting of those pairs 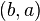 for which
for which 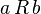 . For example,
. For example, 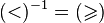 .
.
Let be 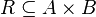 ,
, 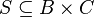 . Composition (or product) of relations
. Composition (or product) of relations  and
and 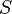 called attitude
called attitude 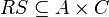 such that:
such that:
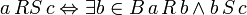 .
.
For example, for a strict order relation on the set of natural numbers, its multiplication by itself is defined as follows: 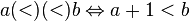 .
.
Binary relations  and
and 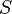 are called permutable if
are called permutable if 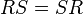 . For any binary relation
. For any binary relation  defined on
defined on 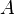 , takes place
, takes place 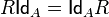 where symbol
where symbol 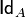 denotes equality defined on
denotes equality defined on 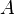 . However equality
. However equality 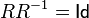 not always fair.
not always fair.
The following identities hold:
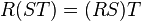 ,
,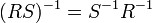 ,
,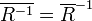 ,
,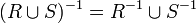 ,
,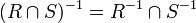 ,
,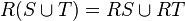 ,
,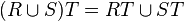 .
.Analogs of the last two identities for the intersection of relations do not exist.
The binary relation between two sets is the correspondence of the elements of one of them to the elements of the second.
Let two sets be given 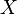 and
and  , let it go
, let it go 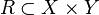 - A subset of their Cartesian products. Then threesome
- A subset of their Cartesian products. Then threesome 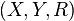 called the binary relation between
called the binary relation between 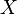 and
and 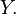 Statement
Statement 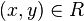 usually written as
usually written as 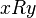 and read "
and read " 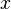 corresponds to
corresponds to 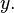 " If a
" If a 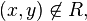 they write
they write 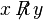 or
or 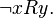
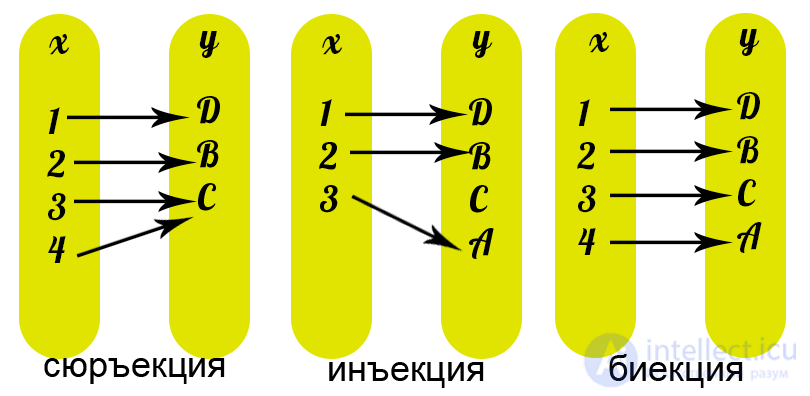
- The mapping f: x-> y is called a SURJECT , if Ay∈Y x∈X: y = f (x). Then y is an image, x is a preimage of y.
- The mapping f: x-> y is called INJECTION , if x 1 ≠ x 2 => f (x 1 ) ≠ f (x 2 ), those different elements of the set X are translated into different elements of the set Y.
or f (x 1 ) ≠ f (x 2 ) => x 1 = x 2
- A mapping f: x-> y is called a bijection if it is both surjective and injective. With a bijective reflection, each element of one set corresponds to exactly one element of another set, and the inverse mapping is defined, which has the same properties.
Binary relation 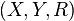 called
called
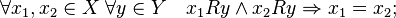
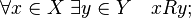
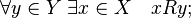
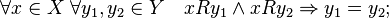
A binary relation on a set is called a partial order relation [1] if it satisfies the properties
Definition A binary relation f is called a function if from Îf and Îf it follows that y = z.
Since functions are binary relations, two functions f and g are equal if they consist of the same elements. The domain of function definition is D f , and the domain of values is R f . They are defined in the same way as for binary relations.
If f is a function, then instead of Îf, they write y = f (x) and say that y is the value corresponding to the argument x , or y is the image of the element x under the mapping f . In this case, x is called the prototype of the element y .
Definition We call f an n-local function from X to Y if f: X n ®Y. Then we write y = f (x 1 , x 2 , ..., x n ) and say that y is the value of the function with the values of the arguments x 1 , x 2 , ..., x n .
Let f: X®Y.
Definition A function f is called injective if for any x 1 , x 2 , y from y = f (x 1 ) and y = f (x 2 ) it follows that x 1 = x 2 , that is, each value of the function corresponds to a single value of the argument.
Definition A function f is called surjective if for every element y Î Y there exists an element x Î X such that y = f (x).
Definition The function f is called bijective if f is both surjective and injective.
Figure 9 illustrates the concepts of relationships, functions, injections, surjections and bections.
 |
Example 9
Consider three functions defined on the set of real numbers and taking on the value in the same set:
Well, take two sets: a lot of students and a lot of chairs in the classroom. And we will establish the correspondence between these two sets, i.e., just sit the students on the chairs.
1. If each student sits in a separate chair (some chairs may remain free), then this is an injection. It is clear that with such a display, the number of chairs cannot be less than the number of students (students cannot sit down two on one chair).
2. If all the chairs were occupied (some may have two or more students), then this is a surjection. In this case, the number of students cannot be less than the chairs.
3. If each student sits on a separate chair, and there are neither free chairs, nor students who lacked chairs, this is a bijection. That is, a bijection is both an injection (each student sits in a separate chair) and a surjection (all chairs are occupied). To be able to display such (bijection) the number of students must be exactly equal to the number of chairs.
Naturally, instead of pupils, chairs can be anything, for example, numerical sets.
All these correspondences can be established between infinite sets. And besides, between the finite and the infinite is an injection, or the infinite and the finite is a surjection.
Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.