Lecture
A planar graph is a graph that can be drawn on a plane without intersecting edges. In other words, a graph is planar if it is isomorphic to some flat graph , that is, the graph depicted on the plane so that its vertices are points of the plane, and the edges are curves on it. The areas into which the graph breaks a plane are called its faces . The unrestricted part of the plane is also a face, the so-called outer face .
For a connected flat graph, the following relation between the number of vertices 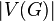 ribs
ribs 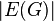 and faces
and faces 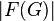 (including outer edge):
(including outer edge):
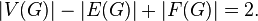
It was found by Euler in 1736 [1] when studying the properties of convex polyhedra. This relationship holds true for other surfaces up to a coefficient called the Euler characteristic. This is an invariant of the surface, for a plane or sphere it is equal to two, and, for example, for a torus - zero.
The formula has many useful consequences. First, all flat layouts of one graph have the same number of faces. Secondly, if each face is bounded by at least three edges (provided that there are more than two edges in the graph), and each edge separates two faces , then
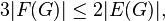
Consequently,
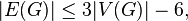
that is, with a larger number of edges, such a graph is obviously non-planar. The converse is not true: the Count Petersen can be taken as a counter-example. It follows that in the planar graph one can always find a vertex of degree at most 5.
The general formula is also easily generalized to the case of a disconnected graph:
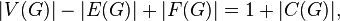
Where 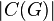 - the number of connected components in the graph.
- the number of connected components in the graph.
Lemma. A full graph with five vertices (K 5 ) cannot be laid on a plane.
Evidence. For it is not performed  .
.

The problem of three wells . There are three houses and three wells. Is it possible to build paths between houses and wells in such a way that a path leads from each house to each well, and no two paths intersect. Bridges can not be built.
Lemma. A full bipartite graph with three vertices in each of the lobes (K 3,3 ) cannot be laid on a plane.
Evidence. According to the formula of Euler, the graph has 5 faces.
On the other hand: any face (including the outer one) contains at least 4 edges. Since each edge is included in exactly two faces, the ratio 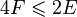 , F is the number of faces, E is the number of edges. We substitute F = 5 and E = 9 into this inequality and see that it does not hold.
, F is the number of faces, E is the number of edges. We substitute F = 5 and E = 9 into this inequality and see that it does not hold.
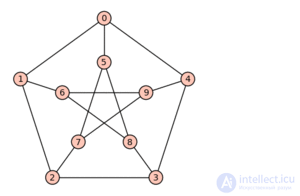
The assertion is obvious: if a graph G contains a subgraph homeomorphic to K 5 or K 3,3 , then it cannot be expanded on a plane. It turns out the opposite is true.
|
The theorem can also be formulated in the following version (sometimes called the “Wagner theorem”).
|
The first algorithm, which finds the Kuratovsky subgraph for linear time, was developed in 1974 by Hopcroft and Tarjan. [2]
Coloring card . It is necessary to color a flat map with a given number of colors so that any two countries that have a common border area have different colors. It turns out that in the absence of enclaves, four colors are always enough, but this statement is extremely difficult to prove, see The problem of four colors.
Rectifying a graph (Fari theorem). Any flat graph can be redrawn so that it remains flat, and the edges become straight.
The graph fits on some surface if it can be drawn on it without intersecting the edges. The laid graph is called geometric , its vertices are points of the plane, and the edges are the lines on it. The areas into which the graph breaks the surface are called faces . Flat graph - a graph laid on a plane.
Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.