Lecture
A direct or Cartesian product of two sets is a set whose elements are all sorted ordered pairs of elements of the original sets.
The concept of a direct product is naturally generalized to the product of sets with an additional structure (algebraic, topological, etc.) since the product of sets often inherits the structures found on the original sets.
| at | at | at | at | at | at | at | at |
|---|---|---|---|---|---|---|---|
| and | and | and | and | and | and | and | and |
| to | to | to | to | to | to | to | to |
| The product of the set {in, and, k} many rainbow colors | |||||||
Let two sets be given 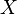 and
and 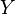 . Direct product set
. Direct product set 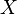 and sets
and sets 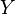 there are so many
there are so many 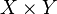 whose elements are ordered pairs
whose elements are ordered pairs  for all kinds
for all kinds 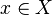 and
and 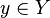 .
.
Displays of the product of sets in its factors -  and
and 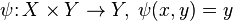 - called coordinate functions .
- called coordinate functions .
The product of a finite family of sets is defined similarly.
Strictly speaking, associative identity 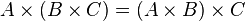 does not take place, but by the existence of a natural one-to-one correspondence between sets
does not take place, but by the existence of a natural one-to-one correspondence between sets 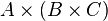 and
and 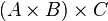 this distinction can often be neglected.
this distinction can often be neglected.
| 000 | 001 | 002 | 010 | 011 | 012 | 020 | 021 | 022 |
| 100 | 101 | 102 | 110 | 111 | 112 | 120 | 121 | 122 |
| 200 | 201 | 202 | 210 | 211 | 212 | 220 | 221 | 222 |
| {0, 1, 2} 3 , 3 3 = 27 elements | ||||||||
|---|---|---|---|---|---|---|---|---|
 -th Cartesian degree set
-th Cartesian degree set 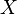 determined for whole non-negative
determined for whole non-negative  , as
, as  -fold Cartesian product
-fold Cartesian product 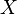 to myself:
to myself:
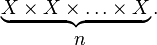
Usually referred to as 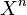 or
or  .
.
With positive  Cartesian degree
Cartesian degree 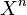 consists of all ordered sets (tuples) of elements from
consists of all ordered sets (tuples) of elements from 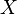 lengths
lengths  . So real space
. So real space  (a set of tuples of three real numbers), there are 3 degree of the set of real numbers
(a set of tuples of three real numbers), there are 3 degree of the set of real numbers 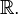
With 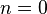 Cartesian degree
Cartesian degree  by definition, contains a single element — an empty tuple.
by definition, contains a single element — an empty tuple.
In general, for an arbitrary family of sets (not necessarily different) 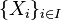 (the set of indices can be infinite) direct product
(the set of indices can be infinite) direct product 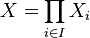 defined as a set of functions that associate each element
defined as a set of functions that associate each element  set element
set element  :
:
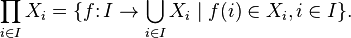
Mappings  called projections .
called projections .
In particular, for a finite family of sets 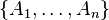 any function
any function  with the condition
with the condition  equivalent to some tuples
equivalent to some tuples  composed of set elements
composed of set elements  so that on
so that on  the second place of the tuple is an element of the set
the second place of the tuple is an element of the set 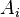 . Therefore, the Cartesian (direct) product of a finite number of sets
. Therefore, the Cartesian (direct) product of a finite number of sets  can be written like this:
can be written like this:
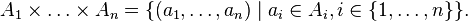
Projections are defined as follows: 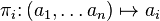
Let be  - mapping from
- mapping from  at
at 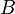 , but
, but 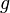 - mapping from
- mapping from 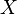 at
at 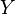 . Their direct product
. Their direct product  called mapping from
called mapping from 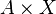 at
at  :
: 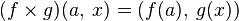 .
.
Similar to the above, this definition is generalized to multiple and infinite products.
Direct (Cartesian) product of two groups  and
and 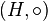 Is a group of all pairs of elements
Is a group of all pairs of elements 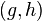 with the operation of component multiplication:
with the operation of component multiplication: 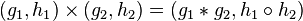 . This group is referred to as
. This group is referred to as 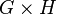 . Associativity of multiplication operations in a group
. Associativity of multiplication operations in a group 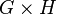 follows from the associativity of operations of multiplied groups. Multipliers
follows from the associativity of operations of multiplied groups. Multipliers 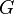 and
and 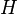 are isomorphic to two normal subgroups of their work,
are isomorphic to two normal subgroups of their work,  and
and  respectively. The intersection of these subgroups consists of one element.
respectively. The intersection of these subgroups consists of one element. 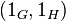 which is a unit of a work group. Coordinate functions of the product of groups are homomorphisms.
which is a unit of a work group. Coordinate functions of the product of groups are homomorphisms.
This definition applies to an arbitrary number of groups multiplied. In the case of a finite number, the direct product is isomorphic to a direct sum. The difference occurs with an infinite number of factors.
In general, 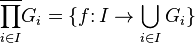 where
where 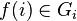 and
and 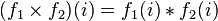 . (The operation on the right side is a group operation
. (The operation on the right side is a group operation 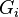 .) The unit of the work group will be a sequence composed of the units of all the groups being multiplied:
.) The unit of the work group will be a sequence composed of the units of all the groups being multiplied: 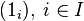 . For example, for a countable number of groups:
. For example, for a countable number of groups: 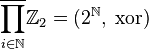 where the right side is the set of all infinite binary sequences.
where the right side is the set of all infinite binary sequences.
Subgroup on the set of all  whose carrier (i.e.
whose carrier (i.e.  ) is finite, called the direct sum . For example, the direct sum of the same set of sets
) is finite, called the direct sum . For example, the direct sum of the same set of sets 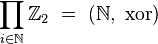 contains all binary sequences with a finite number of ones, and they can be interpreted as binary representations of natural numbers.
contains all binary sequences with a finite number of ones, and they can be interpreted as binary representations of natural numbers.
Similar to the product of groups, it is possible to define the products of rings, algebras, modules and linear spaces, and in the definition of the direct product  (see above) should be replaced with zero. The definition of a product of two (or a finite number) of objects coincides with the definition of a direct sum . However, generally speaking, the direct sum differs from the direct product: for example, the direct product of a countable set of copies
(see above) should be replaced with zero. The definition of a product of two (or a finite number) of objects coincides with the definition of a direct sum . However, generally speaking, the direct sum differs from the direct product: for example, the direct product of a countable set of copies 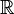 are the space of all sequences of real numbers, whereas the direct sum is the space of those sequences that have only a finite number of non-zero members (so-called finite sequences ).
are the space of all sequences of real numbers, whereas the direct sum is the space of those sequences that have only a finite number of non-zero members (so-called finite sequences ).
Let be 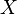 and
and 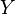 - two topological spaces. Work Topology
- two topological spaces. Work Topology 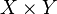 given by the base, consisting of all sorts of works
given by the base, consisting of all sorts of works  where
where 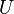 —Open subset
—Open subset 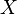 and
and 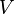 - open subset
- open subset 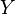 .
.
The definition is easily generalized to the case of the product of several spaces. For infinite work 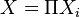 the definition is complicated. Define an open cylinder
the definition is complicated. Define an open cylinder 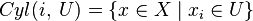 where
where  and
and 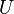 - open subset
- open subset  .
.
The topology of an infinite product will be defined by a base made up of all possible intersections of a finite number of open cylinders (this topology is similar to the compact-open topology of mapping spaces if we take the index set 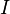 having a discrete topology).
having a discrete topology).
The Tikhonov theorem asserts the compactness of products of any number of compact spaces; however, for infinite products, it cannot be proved without using the axiom of choice (or the assertions of the theory of sets equivalent to it).
Also, Aleksandrov's theorem shows that any topological space can be embedded in the (infinite) product of connected colons, if only the Kolmogorov axiom is fulfilled.
| — | | |
| | — | |
| | | |
| | — | |
The set of vertices of the direct product of two graphs 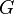 and
and 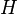 is defined as the product of the vertices of the factor graphs. The edges of the vertices will be connected to the following pairs of vertices:
is defined as the product of the vertices of the factor graphs. The edges of the vertices will be connected to the following pairs of vertices:
 where
where 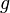 and
and  - connected by the edge of the top of the graph
- connected by the edge of the top of the graph 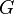 , but
, but  - arbitrary vertex of the graph
- arbitrary vertex of the graph 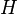 ;
; 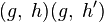 where
where 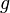 - arbitrary vertex of the graph
- arbitrary vertex of the graph 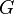 , but
, but  and
and  - connected by the edge of the top of the graph
- connected by the edge of the top of the graph 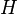 .
. In other words, the set of edges of a graph product is the union of two products: the edges of the first to the vertices of the second, and the vertices of the first to the edges of the second.
The idea of direct work was further developed in the theory of categories, where it served as the basis for the concept of the product of objects . Informally, the product of two objects  and
and 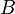 - this is the most common object in this category for which there are projections on
- this is the most common object in this category for which there are projections on  and
and 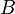 . In many categories (sets, groups, graphs, ...) the product of objects is precisely their direct product. It is important that in most cases it is important not so much a specific definition of a direct work, as the above property of universality. Different definitions will give isomorphic objects.
. In many categories (sets, groups, graphs, ...) the product of objects is precisely their direct product. It is important that in most cases it is important not so much a specific definition of a direct work, as the above property of universality. Different definitions will give isomorphic objects.
// C #
using System;
using System.Collections.Generic;
using System.Text;
namespace mz
{
class program
{
static void Main (string [] args)
{
Console.WriteLine ("Enter the number of elements in the first and second sets, respectively:");
int xcount = Convert.ToInt32 (Console.ReadLine ());
int ycount = Convert.ToInt32 (Console.ReadLine ());
string [] X = new string [xcount];
string [] Y = new string [ycount];
Console.WriteLine ("Enter the elements of the first set:");
for (int i = 0; i <xcount; i ++)
X = Console.ReadLine ();
Console.WriteLine ("Enter the elements of the second set:");
for (int i = 0; i <ycount; i ++)
Y = Console.ReadLine ();
XY xy = new XY ();
string [] s = xy.MulXY (X, Y);
Console.WriteLine ("Result:");
xy.PrintMulXY (s);
Console.ReadLine ();
}
}
public class XY
{
public string [] MulXY (string [] X, string [] Y)
{
string [] res = new string [X.Length * Y.Length];
int k = 0;
foreach (string i in X)
foreach (string j in Y)
{
res [k] = "(" + i + "," + j + ")";
k ++;
}
return res;
}
public void PrintMulXY (string [] strMulXY)
{
foreach (string s in strMulXY)
Console.WriteLine ("{0}", s);
return;
}
}
}
In C ++, using STL.
Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.