Lecture
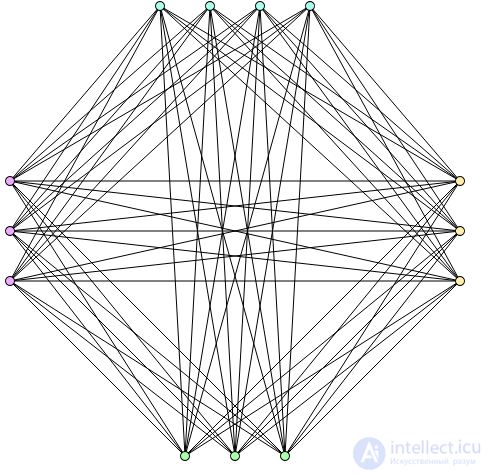
Graf Turana T (13,4) as an example of a kograf
In graph theory, a kograph , or an additionally reducible graph , or a graph free from P 4, is a graph that can be obtained from a graph with a single vertex K 1 by complementing and combining graphs. Thus, a family of cographers is the smallest class of graphs containing K 1 and closed with respect to addition and union.
Kografy opened independently by several authors, since the 1970s. The earliest references can be found in Yang (Jung 1978) , Lerchs (Lerchs 1971) , Zainshe (Seinsche 1974) and Sumner (Sumner 1974) . These graphs were called D * -graphs (Jung 1978) , hereditary Dacey graphs (after the work of James C. Dacey, Jr.) on orthomodular lattices. See Sumner 1974 ) and graphs with two descendants of Barlet and Uri (Burlet, Uhry 1984) .
See the book of Brandnstedt, Lee, and Spinrad (Brandstädt, Le, Spinrad 1999) , where coographers are discussed in more detail, including the facts presented here.
Any kograf can be built using the following rules:
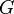 - kograf, then its addition
- kograf, then its addition 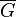 also kograf;
also kograf;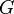 and
and 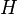 - cographers, their unrelated association
- cographers, their unrelated association 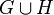 also kograf.
also kograf.Several other descriptions of cographers can be given. Among them:
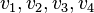 , if a
, if a 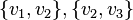 and
and 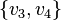 - the edges of the graph, then at least one of
- the edges of the graph, then at least one of 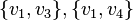 or
or 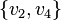 is also a rib (Corneil, Lerchs, Burlingham 1981) .
is also a rib (Corneil, Lerchs, Burlingham 1981) .All full graphs, full bipartite graphs, threshold graphs and Turan graphs are co-graphs. Any kograf is a distance-inheritable perfect comparability graph.
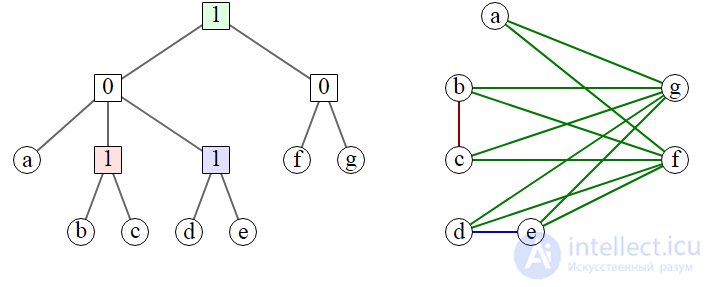
Codes and related kografy. Each edge ( u , v ) in a cograph has the corresponding color of the nearest common parent of the vertices u and v in the coder.
A Koderevo is a tree in which internal vertices are labeled with the numbers 0 and 1. Any code tree T defines a kograf G that has leaves of the Koderev T as vertices, and a subtree that has a root at T , corresponds to a generated subgraph in G defined by a set of descendants this vertex:
The equivalent way to construct a kograf from a koderev is that two vertices are connected by an edge if and only if the smallest common ancestor of the corresponding leaves is marked 1. And vice versa, any kograf can be represented by a coder in this way. If we require that all the tags on all the chains from the root to the leaves alternate, such a presentation would be the only one (Corneil, Lerchs, Burlingham 1981) .
A cograph can be recognized in linear time and can be constructed as a coded-tree representation, if modular decomposition [en] (Corneil, Perl, Stewart 1985) , purification of decomposition [en] (Habib, Paul 2005) or splitting decomposition (Gioan, Paul 2008 ) . Once the codec has been built, many familiar problems of graph theory can be solved by going from the bottom up to the codec.
For example, to find the maximum click in a cograph, we calculate, passing from bottom to top, the maximum click in each subgraph represented by the subtree of the tree. For each vertex with label 0, the maximum click is the maximum click received from the descendants of the top. For a vertex with label 1, the maximum click will be the union of the clicks calculated for the descendants of the vertex, and the size of this click is equal to the sum of the click dimensions. Thus, alternately taking the maximum size and summing the values for each vertex of the tree, we calculate the maximum size of the click, and alternately choosing the maximum click and combining, we construct the maximum click itself. A similar bottom-up passage approach allows us to obtain the maximum independent set, chromatic number, maximum clique coverage, and the existence of the Hamiltonian path [en] in linear time. You can also use codelines to determine in linear time whether two kographs are isomorphic.
If H is a generated subgraph of a kograf G , then H itself is a kograf. The Koderevo for H can be obtained by removing a part of the leaves from the Kodereva for G followed by the merging of vertices with a single descendant. It follows from Kruskal’s trees theorem that the relation to be generated by a subgraph is a good quasi-order on cographs (Damaschke 1990) . So, if a family of kografs (such as planar kografs) is closed with respect to the operation of constructing a generated subgraph, then it has a finite number of forbidden generated subgraphs [en] . From the point of view of computations, this means that checking whether a graph belongs to such a family can be performed in linear time if you use a bottom-up pass through the coder of the given graph.
Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.