Lecture
Combinatorics is a branch of mathematics dedicated to solving problems of choosing and arranging elements of a certain set in accordance with given rules. Combinatorics studies combinations and permutations of objects, the location of elements with given properties. The usual question in combinatorial problems: how many ways ...
The combinatorial tasks also include the tasks of constructing magic squares, the tasks of decoding and encoding.
The birth of combinatorics as a branch of mathematics is associated with the works of the great French mathematicians of the 17th century Blaise Pascal (1623–1662) and Pierre Fermat (1601–1665) on the theory of gambling. These works contained principles for determining the number of combinations of elements of a finite set. Since the 50s of the 20th century, interest in combinatorics has been reviving due to the rapid development of cybernetics.
The basic rules of combinatorics are the sum rule and the work rule .
If some element A can be chosen in n ways, and element B can be chosen in m ways, then the choice of “either A or B” can be done in n + m ways.
For example, If there are 5 apples and 6 pears on a plate, then one fruit can be selected 5 + 6 = 11 ways.
If element A can be chosen in n ways, and element B can be chosen in m ways, then the pair A and B can be selected in n • m ways.
For example, if there are 2 different envelopes and 3 different stamps, then the envelope and stamp can be selected in 6 ways (2 • 3 = 6).
The product rule is true also in the case when the elements of several sets are considered.
For example, if there are 2 different envelopes, 3 different stamps and 4 different cards, then you can choose an envelope, a stamp and a card in 24 ways (2 • 3 • 4 = 24).
The product of all natural numbers from 1 to n inclusive is called n-factorial and is denoted by the symbol n!
n! = 1 • 2 • 3 • 4 • ... • n.
For example, 5! = 1 • 2 • 3 • 4 • 5 = 120.
It is considered to be 0! equal to 1.
The number of permutations of n is equal to n!
For example, if there are 3 balls - red, blue and green, then you can put them in a row in 6 ways (3 • 2 • 1 = 3! = 6).
Sometimes a combinatorial problem is solved by building a tree of possible options .
For example, we solve the previous problem about 3 balls by building a tree.

Workshop on solving problems in combinatorics.
TASKS AND SOLUTIONS
1. In a vase there are 6 apples, 5 pears and 4 plums. How many options to choose one fruit?
6 + 5 + 4 = 15
Answer : 15 options.
2. How many options are there for buying a single rose if they sell 3 scarlet, 2 scarlet and 4 yellow roses?
3 + 2 + 4 = 9
Answer : 9 options.
3. Five roads lead from city A to city B, and three roads lead from city B to city C. How many paths passing through B lead from A to C?
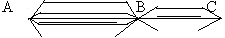
5 • 3 = 15
Answer : 15 ways.
4. How many ways can you make a pair of one vowel and one consonant of the word "shawl"?
vowels: a, o - 2 pcs.
consonants: p, l, t, c - 4 pcs.2 • 4 = 8
Answer : 8 ways.
5. How many dance couples can you make from 8 boys and 6 girls?
6 • 8 = 48
Answer : 48 pairs.
6. In the dining room there are 4 first courses and 7 second. How many different lunch options can I order?
4 • 8 = 28
Answer : 28 options.
7. How many different two-digit numbers can be compiled using the numbers 1, 4 and 7, if the numbers can be repeated?
1 digit - 3 ways
2 digit - 3 ways
3 digit - 3 ways3 • 3 = 9
Answer : 9 different two-digit numbers.
8. How many different three-digit numbers can be compiled using the numbers 3 and 5, if the numbers can be repeated?
1 digit - 2 ways
2 digits - 2 ways
3 digit - 2 ways2 • 2 • 2 = 8
Answer : 8 different numbers.
9. How many different two-digit numbers can be made up of numbers 0, 1, 2, 3, if the numbers can be repeated?
1 digit - 3 ways
2 digits - 4 ways3 • 4 = 12
Answer : 12 different numbers.
10. How many three-digit numbers exist that have all the numbers even?
Even numbers - 0, 2, 4, 6, 8.
1 digit - 4 ways
2 digits - 5 ways
3 digit - 5 ways4 • 5 • 5 = 100
Answer : there are 100 numbers.
11. How many even three-digit numbers are there?
1 digit - 9 ways (1, 2, 3, 4, 5, 6, 7, 8, 9)
2 digits - 10 ways (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
3 digit - 5 ways (0, 2, 4, 6, 8)9 • 10 • 5 = 450
Answer : there are 450 numbers.
12. How many different three-digit numbers can be made up of three different numbers 4, 5, 6?
1 digit - 3 ways
2 digits - 2 ways
3 digit - 1 way3 • 2 • 1 = 6
Answer : 6 different numbers.
13. In how many ways can you identify the vertices of a triangle using the letters A, B, C, D?
1 vertex - 4 ways
2 top - 3 ways
3 vertex - 2 ways4 • 3 • 2 = 24
Answer : 24 ways.
14. How many different three-digit numbers can be made up of numbers 1, 2, 3, 4, 5, provided that no number repeats?
1 digit - 5 ways
2 digits - 4 ways
3 digit - 3 ways5 • 4 • 3 = 60
Answer : 60 different numbers.
15. How many different three-digit numbers, less than 400, can be made up of numbers 1, 3, 5, 7, 9, if any of these numbers can be used only once?
1 digit - 2 ways
2 digits - 4 ways
3 digit - 3 ways2 • 4 • 3 = 24
Answer : 24 different numbers.
16. In how many ways can a flag be made up consisting of three horizontal stripes of different colors, if there is material of six colors?
1 lane - 6 ways
2 lane - 5 ways
3 lane - 4 ways6 • 5 • 4 = 120
Answer : 120 ways.
17. From the class choose 8 people who have the best results in running. How many ways can you make a team of three people from them to participate in the relay?
1 person - 8 ways
2 people - 7 ways
3 people - 6 ways8 • 7 • 6 = 336
Answer : 336 ways.
18. On Thursday in the first grade there should be four lessons: writing, reading, mathematics and physical education. How many different schedule options can you make for this day?
1 lesson - 4 ways
2 lesson - 3 ways
3 lesson - 2 ways
4 lesson - 1 way4 • 3 • 2 • 1 = 24
Answer : 24 options.
19. In the fifth grade, 8 subjects are studied. How many different schedule options can be made on Monday if there should be 5 lessons on this day and all the lessons are different?
1 lesson - 8 options
2 lesson - 7 options
3 lesson - 6 options
4 lesson - 5 options
5 lesson - 4 options8 • 7 • 6 • 5 • 4 = 6720
Answer : 6720 options.
20. The cipher for the safe is made up of five different numbers. How many different cipher options are there?
1 digit - 5 ways
2 digits - 4 ways
3 digit - 3 ways
4 digit - 2 ways
5 digit - 1 way5 • 4 • 3 • 2 • 1 = 120
Answer : 120 options.
21. In how many ways can 6 people be placed at the table on which 6 devices are placed?
6 • 5 • 4 • 3 • 2 • 1 = 720
Answer : 720 ways.
22. How many variants of seven-digit telephone numbers can be made, if we exclude from them numbers starting with zero and 9?
1 digit - 8 ways
2 digit - 10 ways
3 digit - 10 ways
4 digit - 10 ways
5 digit - 10 ways
6 digit - 10 ways
7 digit - 10 ways8 • 10 • 10 • 10 • 10 • 10 • 10 = 8.000.000
Answer : 8.000.000 options.
23. A telephone exchange serves subscribers whose telephone numbers consist of 7 digits and begin with 394. How many subscribers does this station have?
Phone number 394
10 • 10 • 10 • 10 = 10,000
Answer : 10,000 subscribers.
24. There are 6 pairs of gloves in various sizes. In how many ways can you choose one glove for your left hand and one glove for your right hand so that these gloves are of different sizes?
Left gloves - 6 ways
Right gloves - 5 ways (6 gloves of the same size as the left one)6 • 5 = 30
Answer : 30 ways.
25 Of the numbers 1, 2, 3, 4, 5 are five-digit numbers, in which all the numbers are different. How many such even numbers?
5 digit - 2 ways (two even numbers)
4 digit - 4 ways
3 digit - 3 ways
2 digits - 2 ways
1 digit - 1 way2 • 4 • 3 • 2 • 1 = 48
Answer : 48 even numbers.
26. How many four-digit numbers exist that are composed of odd numbers and are divisible by 5?
The odd numbers are 1, 3, 5, 7, 9.
Of them are divided by 5 - 5.
4 digit - 1 way (digit 5)
3 digit - 4 ways
2 digit - 3 ways
1 digit - 2 ways1 • 4 • 3 • 2 = 24
Answer : 24 numbers.
27. How many five-digit numbers are there in which the third digit is 7, the last digit is even?
1 digit - 9 ways (all but 0)
2 digit - 10 ways
3 digit - 1 way (digit 7)
4 digit - 10 ways
5 digit - 5 ways (0, 2, 4, 6, 8)9 • 10 • 1 • 10 • 5 = 4500
Answer : 4500 numbers.
28. How many six-digit numbers exist that have the second digit - 2, the fourth - 4, the sixth - 6, and all the others - odd?
1 digit - 5 options (from 1, 3, 5, 7, 9)
2 digit - 1 option (digit 2)
3 digit - 5 options
4 digit - 1 option (digit 4)
5 digit - 5 options
6 digit - 1 option (digit 6)5 • 1 • 5 • 1 • 5 • 1 = 125
Answer : 125 numbers.
29. How many different numbers less than a million can be written using the numbers 8 and 9?
Unambiguous - 2
Double digits - 2 • 2 = 4
Three-digit - 2 • 2 • 2 = 8
Four-digit - 2 • 2 • 2 • 2 = 16
Five-digit - 2 • 2 • 2 • 2 • 2 = 32
Six-digit - 2 • 2 • 2 • 2 2 • 2 = 64Total : 2 + 4 + 8 + 16 + 32 + 64 = 126
Answer : 126 numbers.
30. There are 11 people in the football team. You need to choose a captain and his deputy. How many ways can this be done?
Captain - 11 ways
Deputy - 10 ways11 • 10 = 110
Answer : 110 ways.
31. In a class 30 people study. In how many ways can one choose the headman and the person in charge of travel tickets?
Warden - 30 ways
Answer. for tickets - 29 ways30 • 29 = 870
Answer : 870 ways.
32. The campaign involves 12 boys, 10 girls and 2 teachers. How many options for groups of three people on duty (1 boy, 1 girl, 1 teacher) can be made?
12 • 10 • 2 = 240
Answer : 240 ways.
33. How many combinations of the four letters of the Russian alphabet (in the alphabet are only 33 letters) can you make, provided that the 2 adjacent letters are different?
1 letter - 33 ways
2 letter - 32 ways
3 letter - 32 ways
4 letter - 32 ways33 • 32 • 32 • 32 = 1.081.344
Answer : 1.081.344 combinations.
Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.