Lecture
The incidence matrix is one of the forms of representation of the graph, in which the links between the incident elements of the graph (edge (arc) and vertex) are indicated. The columns of the matrix correspond to the edges, the rows - to the vertices. A non-zero value in the matrix cell indicates the relationship between the vertex and the edge (their incidence).
In the case of a directed graph, each arc <x, y> is mapped to "-1" in the row of the vertex x and the column of the arc <x, y> and "1" in the row of the vertex y and the column of the arc <x, y>; if there is no connection between vertex and edge, then "0" is put in the corresponding cell.
| Graph | Incidence matrix |
|---|---|
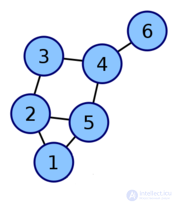 |  |
The adjacency matrix is one way of representing a graph as a matrix.
The adjacency matrix of a graph G with a finite number of vertices n (numbered from 1 to n ) is a square matrix A of size n , in which the value of the element a ij equals the number of edges from the i -th vertex of the graph to the j -th vertex.
Sometimes, especially in the case of an undirected graph, a loop (edge from the i -th vertex to itself) is counted as two edges, that is, the value of the diagonal element a ii in this case is equal to twice the number of loops around the i -th vertex.
The adjacency matrix of a simple graph (free of loops and multiple edges) is a binary matrix and contains zeros on the main diagonal.
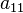 can be considered equal to either one (as shown below) or two.
can be considered equal to either one (as shown below) or two. | Graph | Adjacency matrix |
|---|---|
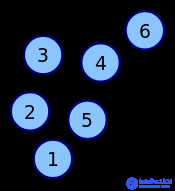 |  |
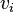 and
and 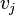 , and in some applications each loop (edge
, and in some applications each loop (edge 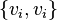 with some
with some 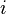 ) counted twice.
) counted twice. The adjacency matrix of an undirected graph is symmetric, and therefore has real eigenvalues and an orthogonal basis of eigenvectors. The set of its eigenvalues is called the spectrum of a graph, and is the main subject of the study of spectral graph theory.
Two graphs G 1 and G 2 with adjacency matrices A 1 and A 2 are isomorphic if and only if there exists a permutation matrix P such that
From this it follows that the matrices A 1 and A 2 are similar, and therefore have equal sets of eigenvalues, determinants and characteristic polynomials. However, the converse is not always true — two graphs with similar adjacency matrices may be non-isomorphic.
If A is the adjacency matrix of the graph G , then the matrix A m has the following property: an element in the i- th row, j- th column is equal to the number of paths from the i -th vertex to the j -th, consisting of exactly m edges.
The adjacency matrix and adjacency lists are the main data structures used to represent graphs in computer programs.
The use of the adjacency matrix is preferable only in the case of non-thinned graphs, with a large number of edges, since it requires storing one data bit for each element. If the graph is sparse, then most of the memory will be wasted on storing zeros, but in the case of unresolved graphs, the adjacency matrix represents the graph in memory rather compactly, using approximately 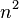 a bit of memory that can be much better than adjacency lists.
a bit of memory that can be much better than adjacency lists.
In algorithms that work with weighted graphs (for example, in the Floyd-Warcil algorithm), the elements of the adjacency matrix, instead of the numbers 0 and 1, indicating the presence or absence of an edge, often contain the weights of the edges themselves. In this case, in place of the missing edges put some special boundary value (English sentinel ), depending on the problem being solved, usually 0 or 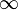 .
.
Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.