The order relation is usually denoted by £. The notation X £ Y means that the pair ( X, y ) belongs to the set A Ì M ´ M , which is an order relation in M , and X precedes Y (or Y follows X ).

The order relation has the properties:

· Reflexivity x £ X ;

· Transitivity; If X £ Y , and Y £ Z , then X £ Z ;

· Antisymmetry; If X £ Y , and Y £ X , then X = Y.

The set on which the order relation is defined is called Ordered , and it is said that the order is introduced by this relation.

If for any two elements X and Y of the set M, the relation X £ Y (or Y £ X ), then M - Completely (linearly) orderly .

For example , a set of natural or real numbers with a natural ratio of order £ are perfectly ordered.

In the general case, it may turn out that for some pairs ( X, y ) none of the ratios X £ Y and Y £ X does not hold. Such elements are called Incomparable , and the set M is called Partially ordered .

Examples of partial order are the relation “to be a divisor”, the inclusion relation Ì, etc. Thus, the inclusion relation on the set of subsets M I of a certain universe M is reflexive ( M I Ì M I ), transitive (if M I Ì M J , a M J Ì M K , then M I Ì M K ) and antisymmetrically (from M I Ì M J , and M J Ì M I follows M I = M J ), but among all possible subsets there are such that none of the ratios of M I Ì M N , and M N Ì M I It does not take place. Similarly, not all pairs of elements from the set of natural numbers are in the relation “to be a divisor”.

This note discusses one of the most commonly used binary relations, the relationship of order.

1. What is order?

Order plays a huge role in our lives. People throughout history have tried to streamline relations among themselves, the surrounding phenomena. Without order it is impossible to imagine human life. Try to imagine a society in which anarchy reigns or a dictionary in which words are arranged chaotically. But what is order? With some orderings, we are so accustomed that often they are simply not aware of, such as the grammatical order of words in a sentence. This article provides a formal definition of the order used in mathematics.

Definition 1.1 . A binary relation a on a set X is called an order relation if it is transitive :

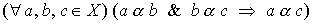
and antisymmetrically :

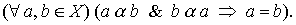
Example 1.1 . Consider the attitude of "older" on many people. Obviously, it is transitive and antisymmetric, and, therefore, is an order relation.

Example 1.2 . The hierarchy of animals, built on the stages of evolution, is a relation of order (Fig. 1).

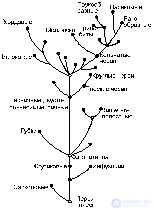
Fig. 1. The main stages of the evolution of eukaryotic organisms

Definition 1.2 . The set X with the order relation defined on it is called an ordered set and is denoted by .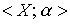

Ordered set 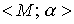with a small number of elements is visually represented as a directed graph. In this case, the elements of the set M are associated with the vertices of the graph (indicated by dots in the figure), and the elements of the relation a with arcs (lines with arrows).

For example, Figure 2 shows a directed graph representing the relation = {( a , a ), ( a , b ), ( a , c ), ( b , c)} on the set M = { a , b , c , d }.

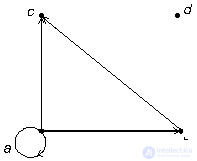
Fig. 2. Graph of an ordered set

You can set the order on the set in various ways. So, for example, in Figure 3 three ways of streamlining the four countries are shown.

Square	Russia	USA	France	England
Population	USA	Russia	France	England
Population density	England	France	USA	Russia

Fig. 3. Three ways to streamline

Figure 4 shows oriented graphs representing the relations "divided" and "less" on the set M = { 1 , 2 , 3 , 4 } of natural numbers.

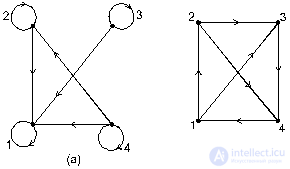
Fig. 4. Graphs of relations "divided" (a) and "less" (b) on the set { 1 , 2 , 3 , 4 }

Example. M = {0; 2; 5; 7}. M2 = {<0; 0>; <0; 2>; <0; 5>; <0; 7>; <2; 0>; <2; 2>; <2; 5>; <2; 7> ; <5; 0>; <5; 2>; <5; 5>;

<5; 7>; <7; 0>; <7; 2>; <7; 5>; <7; 7>}.

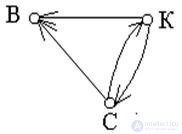
From the set M2, we select a subset R of those pairs in which a> b. R = {<2; 0>; <5; 0>; <5; 2>; <7; 0>; <7; 2>; <7; 5>;}. The set R defines the “more” relation for the elements of the set M. The graph corresponding to this relation is shown in Fig. 5. Each arrow is directed from a larger number to a smaller one.

Fig.

2. Varieties of order relationships

Definition 2.1 . A relation of order a is called a relation of non - strict order on a set X , if a is reflexive :

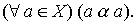
The ratio of non-strict order is usually denoted by the symbol 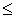. If a 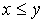, then they say that "the element x precedes the element y " or " y follows x ".

Example 2.1 . Attitude on the set of real numbers is a nonstrict order relation.

Example 2.2 . On the set of subsets of some universal set U, the relation 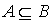is a nonstrict order relation.

Example 2.3 . The relationship of subordination in the institution is not strict order on a set of employees of the institution.

Example 2.4 . Attitude 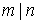( m divides n ) on an arbitrary subset of natural numbers is a non-strict order. Figure 5 shows the graph corresponding to the ordered set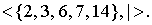

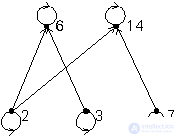
Fig. 5. Graph of a non-strictly ordered set

Example 2.5 . The identity relation is both an equivalence relation and a non-strict order relation.

Definition 2.2 . Two elements 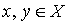are called comparable elements of an ordered set X if either 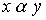either .

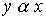The incomparable elements in the ordered set of example 4 are, for example, elements 7 and 2, 2 and 3, 3 and 7.

Definition 2.3 . An order relation a is called a strict order relation on a set X if a is anti-reflexive :

.

A strict order relation is denoted by <.

Example 2.6 . Let f and g be functions with the same domains. We define the relation> as follows: f > g , if for any x from the domain of the function f ( x )> g ( x ). Obviously, this relation is a strict order relation.

For the functions f and g shown in Fig. 6, the relation f > g holds. The pairs of functions f and h , as well as g and h, are incomparable.

Fig. 6. Three functions

Example 2.7 . The alphabetic order is a strict order relation on a set of letters.

Example 2.8 . Let a strictly order relation be given on the set X 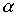. How can you set a strict order relation on a set , that is, how to compare pairs of elements from the set X ? One of the possible options is as follows. On the set X, we define a relation 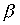condition:

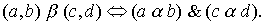
Attitude 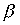is a strict order.

Example 2.9. Another way to set a strict order on a set 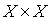is as follows. We assume that the relation ( a , b ) holds 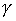( c , d ) if

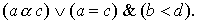
This order relation is called lexicographic . In general, it is defined as follows. For the words v and w of the same length, we assume that v < w , if there exists a number k such that 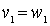, , 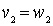..., 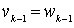, 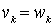where 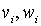- i - th letters of the words v and w, respectively. For words 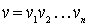and 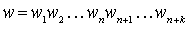( k > 0 ) of different length is considered v < w , if 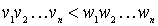or 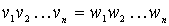and w < v , if 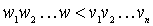. This sorting method is used in dictionaries. In this order, for example:

childhood

Institute

12 <123 <4.

As already noted, it is convenient to represent ordered sets as graphs. Moreover, if 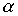is a strictly order relation, then the relation graph a does not contain cycles. The converse is also true: for any graph G without cycles, there exists a relation a of strict order such that the graph associated with this relation coincides with the transitive closure of the graph G. (The transitive closure of a graph G is a graph obtained from a graph G by adding arcs connecting each vertex a with vertices reachable from a .) Indeed, let G be a graph without contours. We define the relation on the set M of vertices of this graph 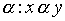if there is a path in the direction of the arcs leading from x to y . It is easy to see that due to the absence of cycles, the relation 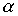is a strict order.

Definition 2.4 . X set with binary relation 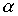called connected if for any two different elements x and y from X either 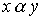either .

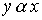Definition 2.5 . A connected order relation on a set X is called a linear order relation.

Example 2.10 . The lexicographical order of words in a dictionary is a linear order.

Example 2.11 . The inclusion relation on a set of figures is not a linear order (Fig. 7).

Fig. 7. Two incomparable figures

Example 2.12 . The attitude of "older" on many people is a linear order.

Example 2.13 . Consider a lot of people. They can be ordered in different ways, for example, by height (Fig. 8).

Fig. 8. The rank

The ordering of the elements of the set X by mapping its elements into some ordered set Y is a fairly typical example of order determination.

The corresponding general method of ordering a set is as follows. Let an injective function be defined on a set X

f : X ® R ,

accepting real numeric values. Set the relation X by the condition: x < y if f ( x ) < f ( y ). Thus, a certain relation is f ( x ) < f ( x ) cannot be. The transitivity and antisymmetry of the relationship Finally, for any pair of different elements x , y from X, either f ( x ) < f ( y ) or f ( y ) < f ( x ) is true, since f is an injection. So the order The function f one-to-one maps our set X onto some subset of the set R of real numbers, so the relation x < y for any elements of the set X is equivalent to the inequality f ( x ) < f ( y ).

Definition 2.6 . Let a strict order relation X be given. The element x X X such that for every y from X that does not coincide with x , the relation x < y ( x > y ) holds is called the smallest ( largest ).

Definition 2.7 . Let a relation of strictly order X. Then the element is called minimal ( maximal ) in the ordered set < X , <> if there is no element y for which y < x (respectively, y > x ).

If, as usual, in the case of x < y, to draw an arrow from x to y , then in the relation graph the minimum element is the one into which the arrows do not enter, and the maximum element from which the arrows do not extend.

In the case of a linear strictly order, the minimal element x has the additional property that for every 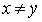done x < y . Thus, for the case of linear orders, the concept of the minimal element coincides with the concept of the smallest element. In the general case, it may turn out that the element x is minimal, but is not in the relation x < y with any other elements. For example, in Figure 5, element 2 is minimal, but not comparable with elements 3 and 7.

To understand the difference between minimal and minimal elements, consider an example.

Example 2.14. Figure 9 shows a diagram of an ordered set, in which there are neither the smallest nor the largest elements, but at the same time there is exactly 1 minimal and exactly 1 maximal elements.

Fig.9. Ordered set

Consider the finite strictly ordered sets in more detail.

Lemma 2.1. If a linear strict order is given on a finite (non-empty) set X , then there exists a smallest element, and it is unique.

Evidence. Take an arbitrary element . If a - the smallest element, then the existence of the desired element is proved. If not, then since 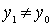, what 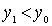. Again either 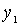- the smallest, or exists 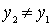such that 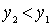. We will continue this process. Suppose that n + 1 elements are already selected for which

.

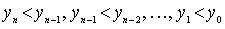By transitivity, it is clear that 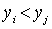with i > j . Hence, due to anti-reflexivity, all the selected elements are not equal in pairs. Therefore, in view of the finiteness of the set X, the selection process must be interrupted in a finite number of steps. Element 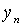, chosen in the last step, will obviously be the desired one. So for any 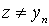done 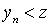. We show that this element is unique. Indeed, let there be another element such that, for everyone 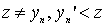. Then simultaneously execute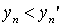d and 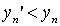that is impossible due to antisymmetry. The lemma is proved.

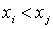Theorem 2.1. Let a relation of linear strict order X. Then on X you can choose this numbering. what's the ratio will be performed if and only if i < j .

Evidence. Let be 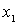- the smallest element in the set X , chosen according to Lemma 1. Denote by 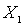lots of 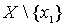. Denote by smallest element of the set 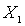. It's clear that 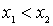. Remove from 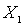element 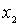and the remaining set is denoted by 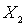. Its smallest element 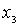satisfies the condition: 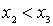. The numbering procedure is already clear: going through all the elements of X sequentially using the indicated method, we will line them up:

,

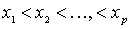where p is the number of elements in X. By virtue of transitivity and antisymmetry, it is clear that 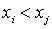if and only if i < j . The theorem is proved.

In essence, this theorem means that any linear strict order on a finite set X is equivalent to the usual order on some segment of the natural series.

The relation of order is directly related to the relation of dominance.

Definition 2.8. Let be 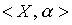is an ordered set, x and y are its elements. We say that x dominates y , if 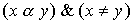but there is no such element z О X that .

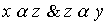With the help of the dominance relation, you can introduce another visual way of representing ordered sets - Hasse diagrams . In the diagrams, each element is represented by a point in the plane, and if y dominates x , then x and y are joined by a segment, with the point corresponding to x located below y .

Consider three partial order relations and construct Hasse diagrams for them.

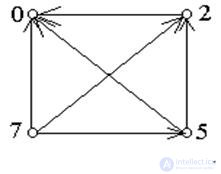
Example 2.15. Let A = { 1 , 2 , 3 }. On the set of all subsets of the set A, consider the relationship "to be a subset". A diagram of this ordered set is shown in Figure 10 (a).

Example 2.16. Let X = { 1 , 2 , 3 , 5 , 6 , 10 , 15 , 30 }. We introduce the relation "divided" on this set. The diagram of this ordered set is shown in Figure 10 (b).

Example 2.17. On the set X = { 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 }, consider the relation of linear order <. His diagram is shown in Figure 10 (c).

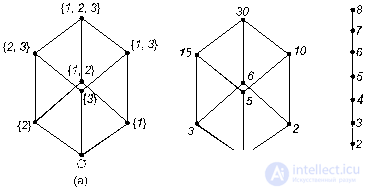
Fig. 10. Hasse diagrams

Note that the Hasse diagrams of the first two relations are the same. This means that these partially ordered sets have the same structure, and this is different from the structure of the third ordered set, although it also contains eight elements. More precisely, such a common structure is defined by the concept of isomorphism.

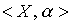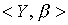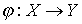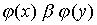Definition 2.9. Two ordered sets and are called isomorphic if there is a bijection preserving the relation of order. In other words, then and only if where 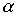and 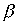- отношения порядка, заданные на множествах X и Y соответственно.

Упорядоченные множества, рассмотренные в примерах 1 и 2 изоморфны.

Теорема 2.2. Всякое нестрого упорядоченное множество 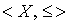изоморфно некоторой системе подмножеств множества X , нестрого упорядоченной отношением включения.

Доказательство. Для каждого элемента 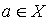рассмотрим множество 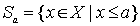. Then 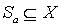and 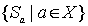- совокупность всех таких подмножеств. Докажем, что эта система подмножеств, нестрого упорядоченная отношением включения, изоморфна . Рассмотрим отображение 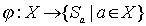такое, что 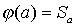. Then - биекция. Действительно, если 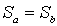, то, поскольку , в силу рефлексивности , имеем 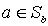and 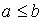. Аналогично получаем 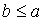и в силу антисимметричности 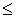имеем a = b , т. е. отображение 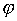инъективно. Besides, 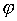сюръективно, так как у любого подмножества 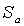есть прообраз a . Докажем теперь, что отображение сохраняет отношение частичного порядка. Пусть 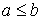. Тогда для любого 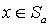из 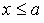в силу транзитивности отношения 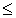следует 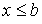, а значит, и . Если 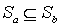, то, поскольку 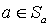, имеем 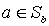, поетому .

Операции над отношениями порядка

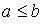Перейдем теперь к обсуждению вопросов, связанных с упорядочением по разным критериям. Пусть у нас имеется несколько отношений порядка. Как по ним построить новое отношение порядка?

Исходя из операций над множествами, мы можем определить ряд операций над отношениями. Далее будем полагать, что все отношения заданы на одном и том же множестве X .

Возьмем два отношения 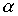and 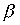. Каждому из них соответствует некоторое множество пар (подмножества 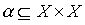and ).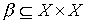

Определение 3.1. Пересечением отношений 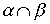называется отношение, определяемое пересечением соответствующих подмножеств. Ясно, что 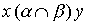выполнено тогда и только тогда, когда одновременно выполнены соотношения 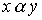и.

Пример 3.1. Пусть X - множество вещественных чисел, a - отношение "быть не меньше", b - отношение "быть строго больше". Then есть отношение "быть строго больше".

Определение 3.2. Объединением отношений называется отношение, определяемое объединением соответствующих множеств. Соотношение 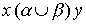выполнено тогда и только тогда, когда выполнено хотя бы одно их соотношений 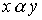or .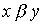

Пример 3.2. Если 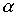- отношение "больше" на множестве чисел, а 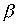- отношение "равно", то 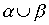- это отношение .

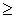Можно ввести операции непосредственно не сводящиеся к теоретико-множественным.

Определение 3.3. Обратным отношением называется отношение, определяемое условием: .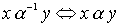

Пример 3.3. Пусть 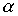- отношение "делит", тогда - отношение "делится".

Определение 3.4. Произведением отношений называется отношение, определяемое следующим образом: соотношение 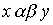равносильно тому, что существует такой элемент 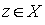, для которого выполнены соотношения 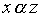and .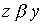

Пример 3.4. Пусть 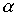- отношение "быть женой", а 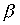- отношение "быть отцом". Что означает в этом случае соотношение 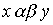? По определению существует такой z , что " x - жена z " и " z - отец y ". Другими словами, " x есть жена отца y ", т.е. " x - мать или мачеха y ".

Пример 3.5. Пусть 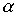- отношение "быть братом", а 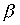- отношение "быть родителем". Тогда произведение 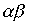есть отношение "быть братом одного из родителей", т.е. "быть дядей".

Прежде чем мы перейдем к теоремам, относящимся к отношению порядка, рассмотрим несколько вспомогательных утверждений (ввиду их простоты мы приводим их без доказательства).

Лемма 3.1. Если отношения 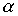and 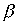рефлексивны, то рефлексивны и следующие отношения:

, , , .

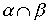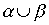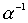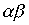Лемма 3.2. Если отношения 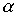and симметричны, то симметричны и следующие отношения:

, , .

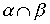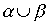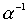Лемма 3.3. Чтобы произведение 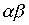симметричных отношений 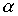and 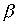было симметрично, необходимо и достаточно, чтобы отношения 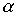and 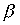коммутировали.

Лемма 3.4. Если отношения a и b - антисимметричны, то антисимметричны также и следующие отношения: , .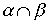

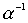Антисимметричность может не сохраняться при объединении и произведении.

Лемма 3.4. Если отношения 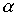and 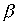транзитивны, то транзитивны также следующие отношения: , .

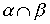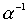Из лемм 3.1, 3.2, 3.3, 3.4 вытекают следующие две теоремы.

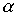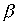Теорема 3.1. Если and - строгие порядки (нестрогие порядки), то пересечение 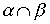также является строгим порядком (нестрогим порядком).

Замечание. Пересечение строгого и нестрогого порядка есть строгий порядок.

The property "to be a linear order" is not required to be maintained at the intersection. This is easiest to see from the following considerations. Let a be a linear order (strict or non-strict), then 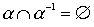(or = E ). Therefore, on a set of more than one element it is not a linear order.

Theorem 3.2. If the relation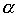is a strict (nonstrict, linear) order, then the relation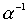is a strict (nonstrict, linear) order.

Combining orders in the general case is not an order. This is clearly seen in this example. Let be 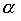a linear weak order, then 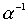there is a relation of the same type. However, association 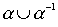is a complete relationship, and, therefore, is not an order. The following are without proof of the conditions under which the union of orders is an order.

Theorem 3.3. If a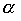 and 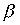- strict orders, the union is a strict order if and only if

.

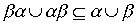Theorem 3.4. In order to combine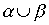weak orders 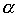and was lax order, it is necessary and sufficient to meet the conditions

,

.

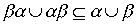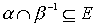Произведение порядков 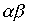также не обязано быть порядком. Это видно из того хотя бы, что для линейного нестрогого порядка 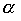произведение

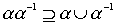
есть полное отношение. Достаточным условием является, например, такое.

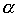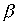Теорема 3.5. Если and - строгие порядки и выполнены соотношения

,

,

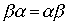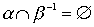то 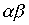- строгий порядок.

Conclusion

В данной лекции мы рассмотрели определения, разновидности и свойства отношений порядка. Однако, при этом не был затронут достаточно важный вопрос, как на практике строить отношения порядка? Этой проблемой занимаются такие разделы математики как теория выбора и принятия решений, теория голосования в больших и малых группах. Указанный вопрос мы рассмотрим в одной из следующих лекций.

LITERATURE

1. Пухначев Ю., Попов Ю. Математика без формул. - М.: АО "Столетие", 1995.

2. Birkhoff G., Barti T. Modern applied algebra. - M .: Mir, 1976.

3. Schrader Yu. A. Equality, similarity, order. - M .: Science, 1971.

4. Nefedov V.N., Osipova V.A. The Course of Discrete Mathematics. - M .: Publishing house of MAI, 1992.

Je. P. Emelchenkov, V. Je. Emelchenkov

THE BINARY RELATIONS. RELATIONS OF ORDER

Abstract. The relation of the order and its characteristics are considered in the a rticle.