Lecture
Let two sets X = { X1, ..., xn } and Y = { Y1, ..., yn } be given. If according to a certain law, each element X Î X is assigned a specific element Y закон Y , then it is said that the mapping of the set X into the set Y is given . Denoted by X ® Y.
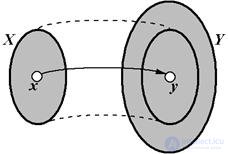
Fig. 1.8 - X®Y mapping
When mapping X to Y, each element X Î X corresponds to one and only one element Y Î Y. This element Y Î Y is called the Image of the Element X Î X , and the element X Î X , in turn, is called the Invoice of the element Y Î Y.
So, when mapping X to Y, each element X Î X has one and only one image Y Î Y. However, it is not at all necessary that every element Y Î Y be the image of some element X Î X. In other words, the preimage Y Î Y does not necessarily belong to the set X.
· If any Y Î Y is an image of at least one X Î X , then they say that there is a mapping of X to Y or a Surgery, or a Cover . Otherwise, it is said that a mapping of X to Y is given .

Fig. 1.9 - Mapping X to Y (Surjection)
If for any two different elements X1, x2 Î X their images y 1 , y 2 Î Y are also different, then they say that a one-to-one mapping X to Y is given Or Injection .

Fig. 1.10 - One-to-one mapping of X to Y (injection)
A mapping that is both an injection and a surjection is called a Mutual-Unique Mapping X on Y or a bijection (overlay).

Fig. 1.11 - One-to-one mapping X on Y (bijection or overlay)
In the general case, when A is mapped to elements X Î X on the set of elements Y Î Y A : X ® Y, the element Y Î Y can be the image of not one, but several ( X1 , ..., Xn ) Î X. The set of elements (all) X1 , ..., Xn Î X , the image of which is given Y Î Y , is called the full prototype of the element Y Î Y and is denoted by A-1 ( Y ).
Let Q be some subset of the set X on which the map A is defined. The set of elements A ( Q ), which are the images of all elements of the set Q , is called the Image of this set And denoted by A ( Q ). In turn, for each set R of Y , its Full preimage A-1 ( R ) is defined as the set of all those elements from X whose images belong to R.
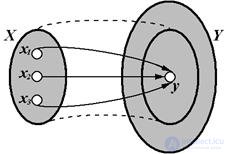
Fig. 1.12 - General display case
Any mapping A of them X to Y is an element of the set P ( X ´ Y ), that is, the set of all subsets of the direct product X ´ Y. The elements of this set are ordered pairs ( X, y ) where X Î X , and Y Î Y.
If F is a one-to-one mapping, and the sets X and Y coincide, then F : X ® X is called the Mapping of the set X onto itself.
The elements ( X, x ) Î X ´ X form the identity mapping E , with F ∙ F -1 = F -1 F = E.
Comments
To leave a comment
Discrete Math. Set theory. Graph theory. Combinatorics.
Terms: Discrete Math. Set theory. Graph theory. Combinatorics.