6. Sorting

When processing data, it is important to know the data information field and its location in the machine.

There are internal and external sorting:

- internal sorting - sorting in RAM;

- external sorting - sorting in external memory.

Sorting is the arrangement of data in memory in a regular form by their keys. Regularity is considered as an increase (decrease) of the key value from the beginning to the end in the array.




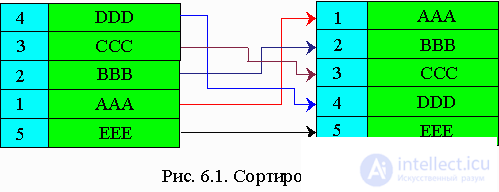
If the sorted records occupy a large amount of memory, then their movement is expensive. In order to reduce them, the sorting is performed in the table of key addresses , the permutation of pointers is performed, i.e. the array itself does not move. This is a method to sort the address table .

When sorting can meet the same keys. In this case, when sorting, it is desirable to arrange after sorting the same keys in the same order as in the source file. This is stable sorting .

The sorting efficiency can be viewed from several criteria:

• 
  time spent on sorting;
• 
  the amount of RAM required for sorting;
• 
  time spent by a programmer to write a program.

We single out the first criterion, since we will only consider sorting methods “ in the same place ”, that is, not reserving additional memory for the sorting process. The equivalent of time spent on sorting can be considered the number of comparisons when performing sorting and the number of movements.

The order of the comparison number when sorting is from O (n log n) to O (n ² ); O (n) is an ideal and unattainable case.

The following sorting methods are distinguished:

• 
  strict (direct) methods;
• 
  improved methods.

Strict methods:

1. 
   direct inclusion method;
2. 
   direct selection method;
3. 
   direct exchange method.

The effectiveness of these three methods is about the same.

6.1. Sort by direct inclusion

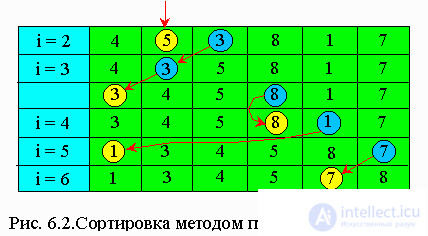
This method is widely used when playing cards. The elements are mentally divided into the ready-made sequence a ₁ , ..., a _i-1 and the original sequence. At each step, starting with i = 2 and increasing i each time by one, the i-th element is extracted from the initial sequence and transferred to the finished sequence, and it is inserted at the right place. In Fig. 6.2 shows as an example the process of sorting by including six randomly selected numbers. The algorithm for this sorting is:


for i = 2 to n

x = a (i)

find a place among a (1) ... a (i) to include x

next i



For sorting by direct inclusion use the following techniques:

Pseudocode: Without barrier : for i = 2 to n x = a (i) for j = i - 1 downto 1 if x <a (j) then a (j + 1) = a (j) else go to L endif next j L: a (j + 1) = x next i return WITH   barrier : for i = 2 to n x = a (i) a (0) = x {a (0) - barrier} j = i - 1 while x <a (j) do a (j +1) = a (j) j = j - 1 endwhile a (j +1) = x next i return

Pascal: Without   barrier : for i: = 2 to n do begin x: = a (i); for j: = i - 1downto 1 do if x <a (j) then a (j +1): = a (j) else goto 1; end; end; 1: a (j + 1): = x; end; end; WITH   barrier : for i: = 2 to n do begin x: = a (i); a (0): = x; {a (0) - barrier} j: = i - 1; while x <a (j) do begin a (j +1): = a (j); j: = j - 1; end; a (j +1): = x; end;

Algorithm efficiency


The number of comparisons of keys Ci with i-th sifting is at most i-1, at least - 1; If we assume that all permutations of N keys are equally probable, then the average number of comparisons = i / 2. The number of shipments Mi = Ci + 3 (including the barrier). The minimum estimates are found in the case of an already ordered initial sequence of elements, while the worst estimates are found when they are initially arranged in the reverse order. In a sense, sorting with inclusion demonstrates true natural behavior. It is clear that the above algorithm describes the process of stable sorting: the order of elements with equal keys with it remains unchanged.

The number of comparisons in the worst case, when the array is sorted in the opposite way, С _max = n (n - 1) / 2, i.e. - O (n ² ). The number of permutations M _max = C _max   + 3 (n-1), i.e. - O (n ² ). If the array is already sorted, then the number of comparisons and permutations is minimal: C _min   = n-1; M _min = = 3 (n-1).