Lecture
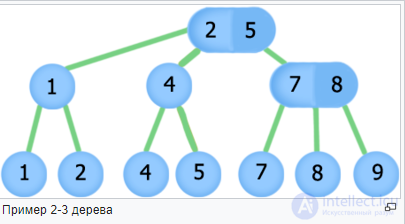
Example 2-3 tree
2-3 tree (Eng. 2-3 tree ) - a data structure that is a balanced search tree, such that two or three branches can go out of each node and the depth of all leaves is the same. It is a special case of B + tree .
2-3 tree - a balanced search tree with the following properties:
We introduce the following notation:
Each tree node has fields:
Initially, . We will look at the keys in the nodes until the node is a leaf. Consider two cases:
T search ( T x):
Node t = root
while (t is not a leaf)
if (t.length == 2)
if (t.keys [0] else
t = t.sons [0]
else if (t.keys [1] else if (t.keys [0] else
t = t.sons [0]
return t.keys [0]
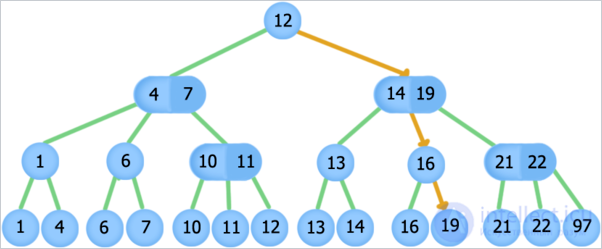
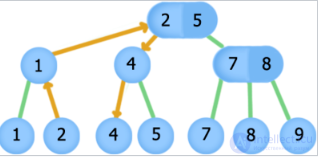
Search for element 19, orange arrows indicate the path through the tree when searching
If the root does not exist - the tree is empty, then the new element will be the root (at the same time as the leaf). Otherwise, proceed as follows:
First, find where the element would be by applying . Next, check if this node has a parent, if it does not, then there is only one element in the tree - the sheet. Take this sheet and the new node, and create a parent for them, arrange the sheet and new node in ascending order.
If the parent exists, then we will hang another son to it. If the sons became , then we divide the parent into two nodes, and repeat the separation now for his parent, because he also could already have sons, and we divided him became son more. (before dividing, we will update the keys).
function splitParent ( Node t):
if (t.length> 3)
Node a = Node (sons = {t.sons [2], t.sons [3]}, keys = {t.keys [2]}, parent = t.parent, length = 2)
t.sons [2] .parent = a
t.sons [3] .parent = a
t.length = 2
t.sons [2] = null
t.sons [3] = null
if (t.parent! = null )
t.parent [t.length] = a
t.length ++
sort sons at t.parent
splitParent (t.parent)
else // we split the root, we need to suspend it to the common parent, which will be the new root
Node t = root
root.sons [0] = t
root.sons [1] = a
t.parent = root
a.parent = root
root.length = 2
sort sons at root
If the sons became , then we do nothing. Next, you need to restore the keys on the way from the new top to the root:
function updateKeys ( Node t):
Node a = t.parent
while (a! = null )
for i = 0 .. a.length - 1
a.keys [i] = max (a.sons [i]) // max - returns the maximum value in the subtree.
a = a.parent // Note: max is easy to find if you store the maximum
// right subtree in each node - this is the value and will be max (a.sons [i])
must be run from a new node. Adding an item:
function insert ( T x):
Node n = Node (x)
if (root == null )
root = n
return
Node a = searchNode (x)
if (a.parent == null )
Node t = root
root.sons [0] = t
root.sons [1] = n
t.parent = root
n.parent = root
root.length = 2
sort sons at root
else
Node p = a.parent
p.sons [p.length] = n
p.length ++
n.parent = p
sort s s u p
updateKeys (n)
split (n)
updateKeys (n)
Since we go down once and go up when we split our parents no more than once, works for .
Examples of adding:
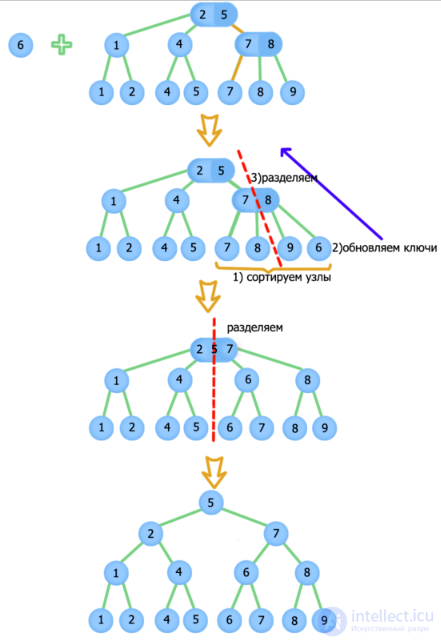
Adding item with key 6
Let initially be the node where .
If does not have a parent, then this is the root (at the same time, it is the only element in the tree). Let's remove it.
If exists, and he has strictly more than sons, then simply remove , and reduce number children.
If the parent two sons, we will consider possible cases (first we delete everywhere:)
We generalize the algorithm when deleting when the parent two sons:
As a result, we get a 2-3 tree that is correct in structure, but we have a violation in the keys in the nodes, fix them using , starting from .
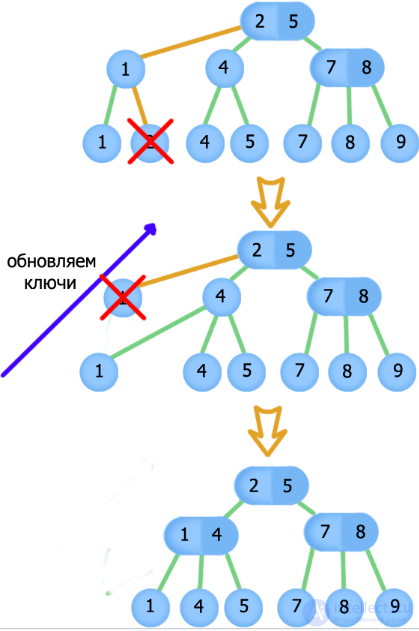
Delete item with key 2
Due to the fact that our nodes are sorted to the maximum in the subtree, the next object is the neighboring sheet on the right. You can get there as follows: we will go up until we have the first opportunity to turn right down. As soon as we turn right down, we will always go left. Thus, we will appear in the next sheet. If we have never been able to turn right down and come to the root, then the next object does not exist. The case with the previous is symmetric.
T next ( T x):
Node t = searchNode (x)
if (t.keys [0]> x) // x was not in the tree, and we found the next one right away
return t.keys [0]
while (t! = null )
t = t.parent
if (can be turned right down)
at t we place the vertex into which we turned
while (while t is not a leaf)
t = t.sons [0]
return t
return t.keys [0]
Path when searching for the next item after 2
B + trees, support the operation , which allows you to find m of the following elements. The naive implementation is as follows: we will call times to search for the next element, this solution works for . But 2-3 trees allow finding the next m elements behind , which greatly speeds up the search for large . By construction, all the leaves are sorted in ascending order, we will use this to find m elements. We need to connect the leaves, for this we modify and . Add the following fields to the nodes:
Let be the added node. Change as follows: at the very end, after we have updated all the keys, we will find and write a link to it at . Similarly with the left.
Let be the node to be deleted. Change as follows: at the very beginning, before deleting , we will find the next and write it in right sheet relative to . With the left we will do the same.
As a result, we have a doubly connected list in the leaves, and in order to display elements, we just need to find the necessary element once and go right to the elements.

Comments
To leave a comment
Structures and data processing algorithms.
Terms: Structures and data processing algorithms.