Lecture
In any state machine, the input signals arrive in a certain sequence in time, so there is a concept of an input sequence. The output sequence is determined similarly . The dependence of the output sequence on the input sequence will be called the condition of the finite state machine.
There are combinational and sequential automatic machines. For combination automata is characterized by the fact that each set of states of the outputs (each input sequence) is uniquely determined by one or more of the finite set of states of the input variables. In addition, each output function is characterized by certain combinations of inputs. In general, the action of such an automaton can be described by some unambiguous functional dependencies between its input and output variables:
y 1 = λ 1 ( x 1 ; x 2 ; ...; x m ),
y 2 = λ 2 ( x 1 ; x 2 ; ...; x m ),
. . .
y n = λ n ( x 1 ; x 2 ; ...; x m ).
Example : Let the input have three variables x 1 ; x 2 ; x 3 . The output is two logical functions y 1, y 2.
Suppose that at the inputs we have the values x 1 = 1, x 2 = 0, x 3 = 1, the values of the outputs with such a set of inputs will be - y 1 = 1, y 2 = 0. If the machine is combinational, then change the combination of its state outputs (say, y 1 = 0, y 2 = 0) is possible only in case of a change in the state of its inputs (suppose x 1 = 1, x 2 = 0, x 3 = 0 or x 1 = 0, x 2 = 0, x 3 = 1). That is, each combination of outputs is uniquely determined by one or another combination of inputs. Then the output function y 1 can be expressed by logical expressions (Boolean functions) defined only by the input variables,
y 1 = x1  x3;
x3;  = x1
= x1 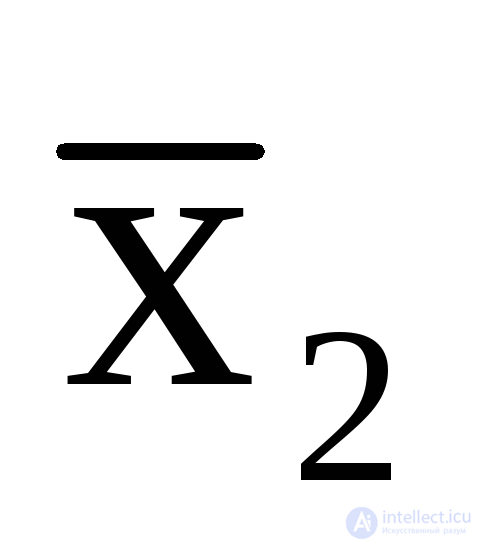
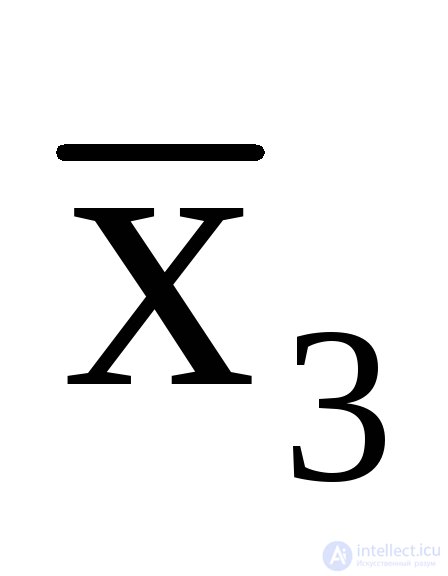
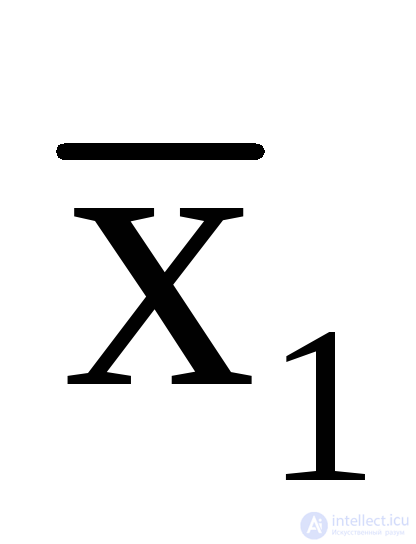
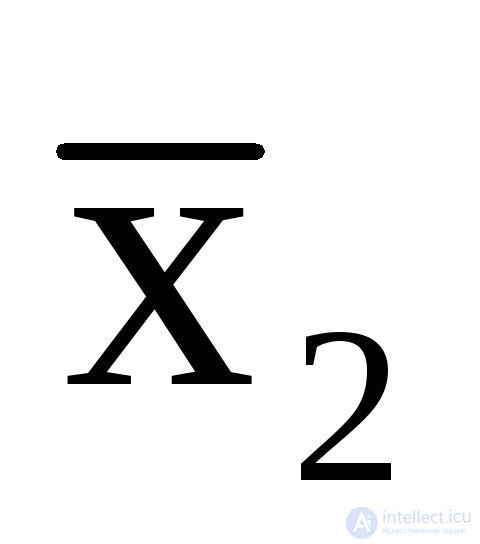 x3,
x3,
or present a truth table (Table 5.9).
Table 5.9
x 1 | x 2 | x 3 | y 1 | y 2 |
one | 0 | one | one | 0 |
one | 0 | 0 | 0 | 0 |
0 | 0 | one | 0 | 0 |
For combinational automata, the transition function does not make sense, since they lack feedback channels (memory), and internal states are determined by the state of the outputs. The function of the outputs in this case degenerates to the form y v = λ ( x v ). Such automata are also called memoryless automata or trivial automata.
Table 5.10 Table 5.11
. x 1 | x 2 | x 3 | y 1 | x 1 | x 2 | x 3 | z | y 1 | ||
one | 0 | 0 | 0 | one | 0 | 0 | 0 | 0 | ||
... | ... | ... | ... | ... | ... | ... | ... | ... | ||
one | 0 | 0 | one | one | 0 | 0 | one | one |
In sequential automata, the same set of states of input symbols can determine different states of output functions at different clock moments of the cycle. For example, at one of the stages of the cycle τ v with a set of inputs x 1 = 1, x 2 = 0, x 3 = 0, the output function y 1 = 0, and at some other stage of the cycle τ v + i with the same set of inputs, the output function y 1 = 1 (table. 5.10).
Thus, the operating conditions of this automaton are contradictory. The various internal states of the automaton in this case are determined not only by the states of the inputs, but also by the sequence of arrival of the input signals. Such an automaton cannot be built without introducing additional internal variables encoding a sequence of processing automaton clock cycles, which will be called memory elements z (tab. 5.11) Variable z It is both an output function and an input variable, but does not change the total number of input variables and, on the block diagram of the automaton, has the form of feedback (Figure 5.1b). In this case, the function y 1 will be defined by the following logical expressions:
y1 = x1 
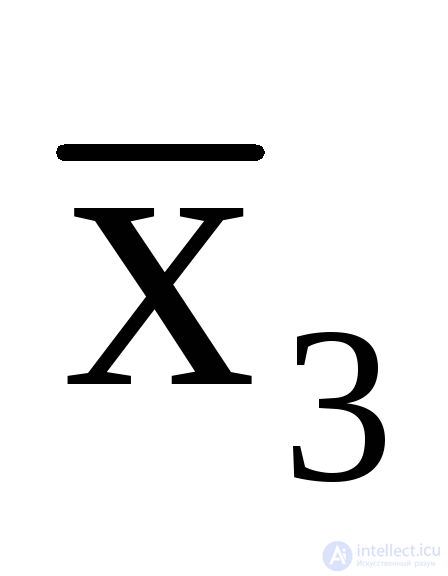
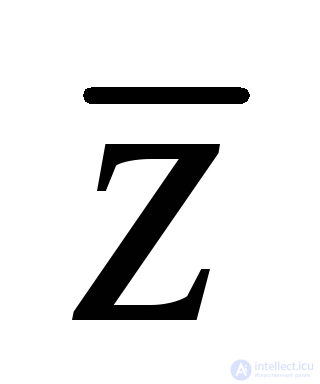 ,
, 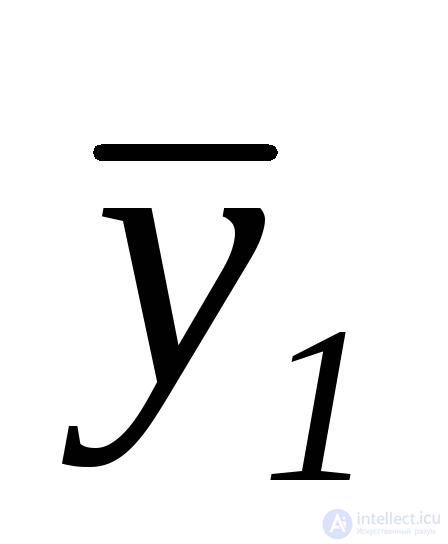 = x1
= x1 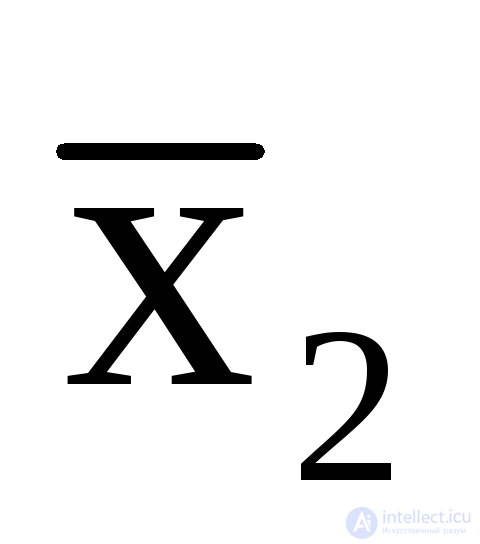
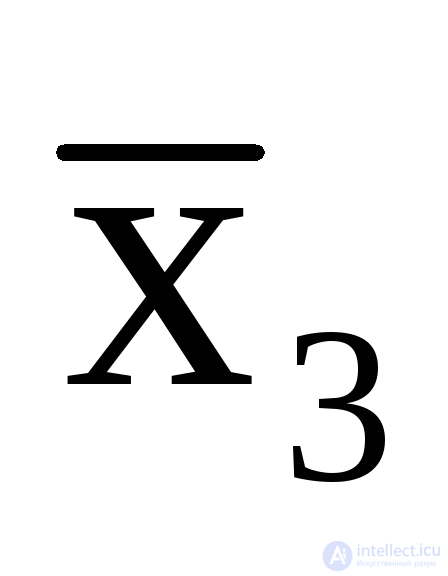 z.
z.
As already mentioned, the presence of memory z determines the internal states of the automaton q v , which, in turn, determine the output function y v along with the states of the inputs x v . Sequential automata are characterized by the presence of transition functions δ and output functions λ.
If the characteristic functions δ and λ are defined for all possible sets from the set X × Q, then such an automaton is called completely defined or complete , that is,
(  q Q) (
q Q) (  x X) (δ ( q , x ) ).
x X) (δ ( q , x ) ).
In practice, there are cases when not every character of the input alphabet can be served on a machine that is in a certain internal state. q v ( restrictions on input ), or its outputs with some input effects are of no interest or do not exist at all ( uncertainty of outputs ). In this case, we deal with incomplete or partial automata, and their exit and transition tables will have some unfilled cells.
The definition of the general model of the automaton, given at the end of section 5.1, is associated with automata of the first kind , which are called Mealy automata. If the output function is determined only by internal states (the state of the memory elements), then we are dealing with automata of the second kind , called Moore automata. Such automata usually model computational processes. The output function of the Moore automaton is determined only by the internal states y v = λ ( q v , ) and is naturally single-argument; it is usually called the function of marks, since for each state it unambiguously associates a mark with an output. In the transition graph, which displays the Moore automaton, the output value is written not at the edge, but at the vertex (see Fig. 5.8a).
Comments
To leave a comment
Finite state machine theory
Terms: Finite state machine theory