Lecture
It is convenient to present the Turing machine in the same way as the state machine using the transition graph. In such a graph, the internal states correspond to the vertices, and the edges that determine the transition from one vertex to another are marked with an input symbol, an output symbol, and the direction of movement of the head (Fig. 6.5).
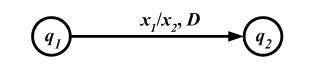
Fig. 6.5
Before starting work, the initial word is applied to the working tape MT and initial conditions are set, i.e. indicates the first cell to be monitored and the initial state. After starting the machine, the process of converting information occurs automatically.
Example 1. Construct an MT recognizing the language {аnсn}. Let the initial configuration of this MT (state q ) correspond to a string of characters <aaassc>, and the head is located opposite the extreme right character of the input string. The transition graph of such an MT is shown in Fig. 6.6.
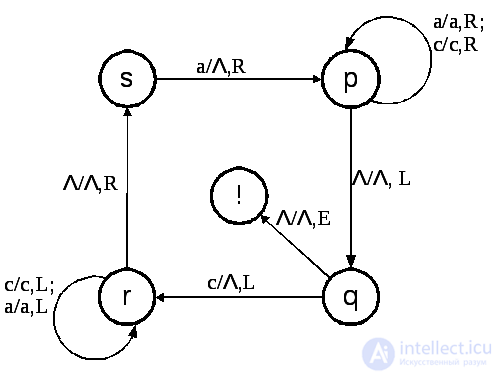
Fig. 6.6
In accordance with the graph, being in the initial state q , the machine head reads the rightmost “c” symbol, replaces it with the empty Λ symbol and shifts left one cell (c / Λ, L). In this case, the machine enters the next state, r , in which characters are read without changing them (c / s, L; a / a, L). As soon as the head of the MT went beyond the limits of the character chain and considered an empty symbol Λ (Λ / Λ, R), the machine head starts to move to the right and the machine changes to the state s , in which the leftmost character “a” is replaced with “Λ” (a / Λ, R). Then MT enters the next state p , in which, by moving the head to the right, it reads the characters without changing them (a / a, R; s / s, R) to the rightmost symbol. Then the process is repeated until all the characters in the specified chain are read and replaced with “Λ”, and the MT is in the “!” State.
Example 2. Consider the MT, which produces the addition of two numbers. We agree to represent natural numbers in a single (unary) code, i.e., for all numerical functions, the alphabet of the initial data is Xish = {1} and the integer n is represented by the word 1 ... 1 = 1 n consisting of n ones.
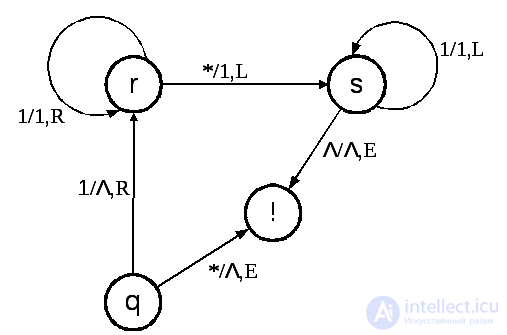
Fig. 6.7
Let, for example, you want to add the numbers 4 and 6. In the previously introduced representation of numbers, add the numbers m and n - this means the word 1m * 1 n is processed into the word 1m + n , i.e. remove the separator * and move one of the addends, say the first, to another. The initial word on the tape is written as 1111 * 111111, and the initial configuration is determined by the position of the head in the cell with the leftmost unit and state q . This transformation is performed by MT + with four states with the transition graph shown in Fig. 6.7.
Following the transition graph, the unit erases at the first cycle, a command to shift to the right and a transition to the state r (1 / Λ, R) is issued . In this state, the units are read without changing them and a successive shift to the right through all units (1/1, R) to the separator "*". Then, instead of a separator, the unit fits into the cell and the machine goes to the state s , starting to move the head to the left (* / 1, L). Having reached the first empty cell, the machine stops, turning into the “!” State. As a result, we obtain the word 1111111111, corresponding to the number 10. The transition (* / Λ, R) from the state q to “!” Is provided for the case when a = 0 and the source word has the form “* 1 n ”.
Example 3. Consider the MT, which produces the definition of the greatest common divisor of two positive integers specified in the unary code. Let two numbers be given m = 4 and n = 6. The initial configuration of the machine in the initial state q corresponds to the position of the head on the extreme right symbol of the number m (Fig. 6.8)
Fig. 6.8
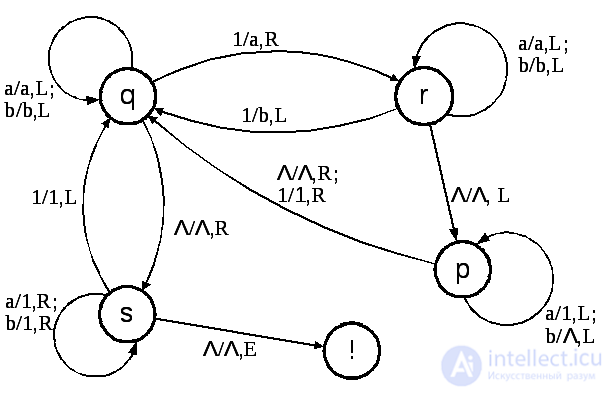
Fig. 6.9
We provide the reader to independently analyze all the intermediate configurations of MT in the process of working out the algorithm on the transition graph (Fig. 6.9). In the process of working out the algorithm, auxiliary intermediate symbols a and b are used .
The algorithm for calculating the GCD of two numbers here consists in repeating actions to find the smallest of two numbers and subtract it from the larger one until equal numbers are obtained.
The Turing machines described are specialized: each algorithm has its own machine. Considering the functional diagram as a program description, one can come to the concept of a universal Turing machine, which implements any algorithm, if the corresponding program is recorded on its tape, besides the initial data. Thus, the intuitive concept of an algorithm gets a precise definition as a process that can be represented by a functional diagram and implemented by a Turing machine.
Control tasks
1. Build a Turing machine that recognizes Dick's language - the bracket skeletons of arithmetic expressions. Examples of chains of this language:
“(())”; “(()) ((() ()))”
2. Construct an MT recognizing the language a n ↑ 2. Examples of chains of this language: " a "; " Aaaa ."
Note: Use the relation: (k + 1) 2 = k2 + 2k + 1 or the fact that the square of a natural number is represented as the sum of consecutive odd numbers (22 = 1 + 3; 32 = 1 + 3 + 5; 42 = 1 + 3 + 5 + 7, etc.)
3. Construct an MT recognizing a language whose chains contain the same number of occurrences of the symbols a, b, c . An example of a chain of this language: “ b a a c b c c b a”
4. Build MT, increasing binary numbers by one.
5. Build an MT that reduces binary numbers by one.
6. Build an MT converting a binary number to a unary form, and vice versa, from a unary form to a binary representation.
7. Build an MT that converts a number from the five-fold number system to the seven-dimensional one.
8. Build an MT that converts a number from binary to octal number system.
9. Build an MT that converts a number from binary to decimal.
10. Build MT, counting the product of two given numbers in a unary record.
11. Construct MT summing 1 to the number written in the ternary notation.
12. The tape contains the number x in the ternary notation. Build an MT, recording the number “2 x” on a tape , if x is divided into three without a remainder, and “ x - 1” - otherwise.
13. For natural numbers given as words in the alphabet 0, | , define the multiplication operation and construct the MT over the alphabet 0, | , which for any natural numbers m and n calculates their product.
14. Build MT over the alphabet а, b, which:
a) to any word х а, b appends to the left (right) the given word w 0 ;
b) recognizes double words in the alphabet а, b;
c) doubles an arbitrary word x а, b, i.e. This word calculates the word xx.
Comments
To leave a comment
Finite state machine theory
Terms: Finite state machine theory