Lecture
The Boolean function (X1, X2, ..., Xn) is an n- local function, the arguments and values of which belong to the set {0,1}.
If logical statements can be true or false, then for a Boolean function, the analogs of these values are 1 or 0. Truth tables and basic equivalences of propositional algebra are valid for Boolean functions.
Additionally, operations are entered:
X1 | X2 = X1∧X2 - Sheffer's stroke and
X1 ↓ X2 = X1vX2- Pierce arrow.
|
X1 |
X2 |
¬X1 |
X1∧X2 |
X1vX2 |
X1⇒X2 |
X1⇔X2 |
X1 | X2 |
X1 ↓ X2 |
|
one |
one |
0 |
one |
one |
one |
one |
0 |
0 |
|
one |
0 |
0 |
0 |
one |
0 |
0 |
one |
0 |
|
0 |
one |
one |
0 |
one |
one |
0 |
one |
0 |
|
0 |
0 |
one |
0 |
0 |
one |
one |
one |
one |
We give the definitions necessary to define Boolean functions.
An elementary conjunction (disjunction) is a logical product (sum) of any number of independent logical variables entering it with or without inversion no more than once. The number of input variables is called the rank of an elementary conjunction (disjunction).
Elementary conjunctions (disjunctions) of the same rank, containing the same variables, but differing by the sign of the inversion of one of the variables, are called neighbors .
The disjunction of any number of elementary conjunctions is called the disjunctive normal form (DNF), for example:
(  b
b  ) (
) ( 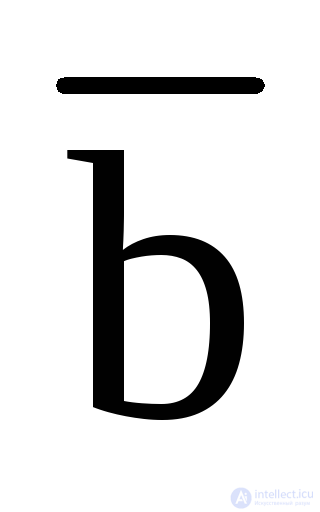 c)
c)  or
or  b
b  +
+ 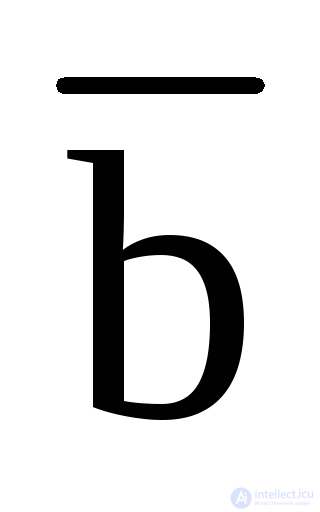 c +
c +  .
.
A conjunction of any number of elementary disjunctions is called a conjunctive normal form (CNF), for example:
(a b  ) (
) ( 
 d) (
d) ( 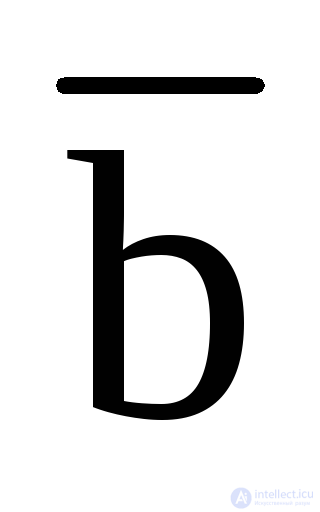
 ) or (a + b +
) or (a + b +  ) (
) (  +
+  + d) (
+ d) ( 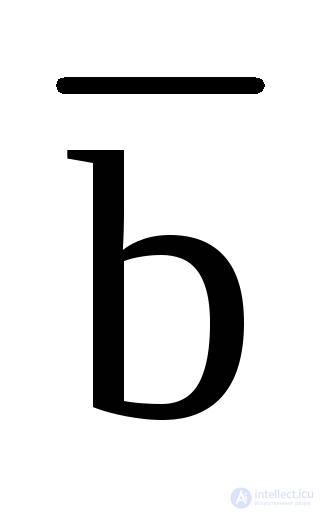 +
+  ) (hereinafter, to simplify the perception of Boolean functions, we will use the second type of record).
) (hereinafter, to simplify the perception of Boolean functions, we will use the second type of record).
Decomposition theorems (see § 2.2) can be applied to all variables defining a Boolean function, then, for example, using the first decomposition theorem for the function of three variables f (a, b, c), we get:
f (a, b, c) = a · b · c · f (1,1,1) +  · B · c · f (0,1,1) + a ·
· B · c · f (0,1,1) + a · 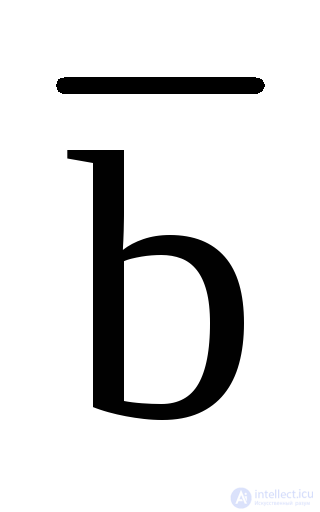 · C · f (1,0,1) + a · b ·
· C · f (1,0,1) + a · b ·  · F (1,1,0) + +
· F (1,1,0) + +  ·
· 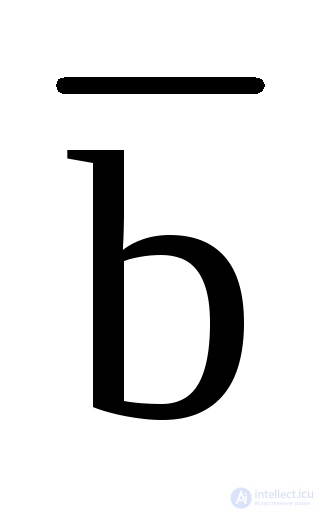 · C · f (0,0, 1) +
· C · f (0,0, 1) +  · B ·
· B ·  · F (0,1,0) + a ·
· F (0,1,0) + a · 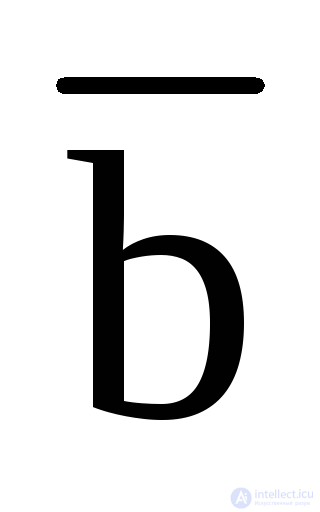 ·
·  · F (1,0,0) +
· F (1,0,0) +  ·
· 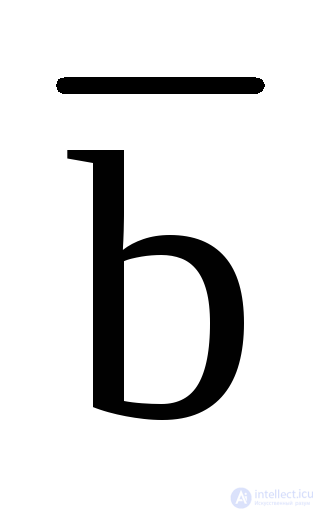 ·
·  · F (0,0,0).
· F (0,0,0).
Each elementary conjunction of this expression is composed of a set of all variables in direct or inverse form and some coefficient that takes the value of the function, if in it we set equal to one the direct value of the corresponding variable, and zero - the inverse. It is easy to see that in this case, according to the law of the zero set, elements with a zero value of the function will vanish and only the sets of variables will remain with a single value of the function, which we will further call constituents of the decomposition of the unit , or minthroms .
If we apply the second decomposition theorem, we obtain the form of decomposition of a function into constituents of zero:
f (a, b, c) = [a + b + c + f (0,0,0)] [  + b + c + f (1,0,0)] [a +
+ b + c + f (1,0,0)] [a +  + c + f (0,1,0] [a + b +
+ c + f (0,1,0] [a + b +  + + f (0,0,1)] [
+ + f (0,0,1)] [  +
+ 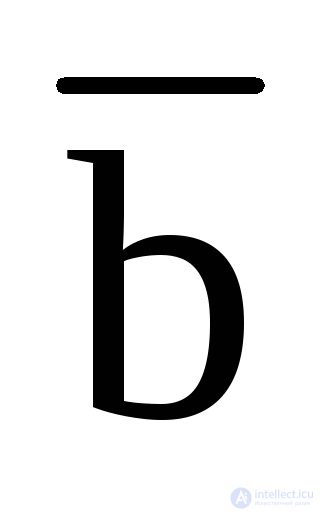 + c + f (1,1,0)] [
+ c + f (1,1,0)] [  + b +
+ b +  + f (1,0,1)] [a +
+ f (1,0,1)] [a + 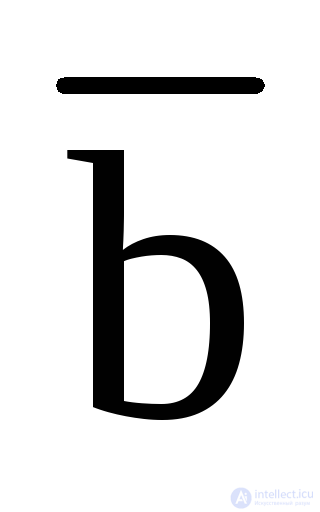 +
+  + f (0,1,1)] [
+ f (0,1,1)] [  +
+ 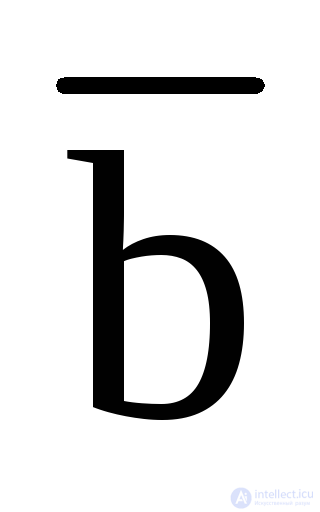 + +
+ +  + f (1,1,1)].
+ f (1,1,1)].
Here, according to the law of the universal set, each elementary disjunction with a single value of a function also takes a single value, and as a result only those disjunctions of variables remain, the inverse values of which determine the zero value of the function. These disjunctions are called constituents of zero expansion , or maxstermes . Such decomposition methods extend to functions with any number of variables.
Expanding the boolean functions on the constituents, we get the so-called. perfect forms. The perfect disjunctive form (SDNF) is the disjunction of the constituents of the unit (minterms), and the perfect conjunctive form is the conjunction of the constituents of the zero (magsterms).
Any arbitrarily complex Boolean function can be converted to DNF or CNF, and then into perfect forms (CDNF or SKNF). To do this, it is necessary first of all, using the de Morgan theorem, to exclude inversions over functions, going to forms in which there are inversions only over single variables. Then, using the laws of Boolean algebra, bring logical expressions to disjunctive or conjunctive forms. The concept of perfect forms is used in minimizing functions and to determine equivalence. Two Boolean functions are considered equivalent if their SDNF and SKNF completely coincide.
|
Variables |
Function |
Decimal equivalent |
|||
|
a |
b |
c |
d |
Y |
|
|
0 |
0 |
0 |
0 |
one |
0 |
|
0 |
0 |
0 |
one |
one |
one |
|
0 |
0 |
one |
0 |
0 |
2 |
|
0 |
0 |
one |
one |
one |
3 |
|
0 |
one |
0 |
one |
one |
five |
|
0 |
one |
one |
one |
0 |
7 |
|
one |
0 |
0 |
0 |
one |
eight |
|
one |
0 |
0 |
one |
0 |
9 |
|
one |
one |
0 |
one |
0 |
13 |
|
one |
one |
one |
one |
0 |
15 |
Table 2.1 One of the most common forms of representation of Boolean functions is a truth table (state table). The truth table determines the value of the function for all possible states of the input variables. Since any logical variable can take only two values — 0 and 1, for the Boolean function “n” of the input variables the number of values will be determined by the exponential function 2n.
A function is fully defined if its values (0 or 1) are known for any set of input variables.
A boolean function is not fully defined (incomplete) if there is one or several sets of variables for which the value of the function is not defined (it can be either 0 or 1) or it does not exist. Such function values are called fictitious (F). An example of the job is not fully defined functions are presented in Table. 2.1.
Each set of logical variables is represented by a binary number of the nth digit, and, therefore, it corresponds to a certain decimal number. The decimal number corresponding to the binary set of logical variables is called the decimal equivalent . Thus, a boolean function can be represented using decimal equivalents:
Y1 = {0,1,3,5,8}; Y0 = {2,7,9,13,15}.
The remaining sets that are not specified by the truth table are likely to be fictitious YF = {4,6,10,11,12,14}.
According to the truth table, you can get perfect forms for writing boolean functions. So, for recording in the form of SDNF, it is necessary to select from the table single sets of variables, to represent them in the form of unit constituents and to make them disjunction.
PDNF: Y = 
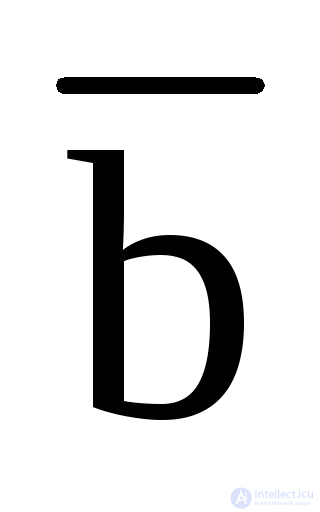

 +
+ 
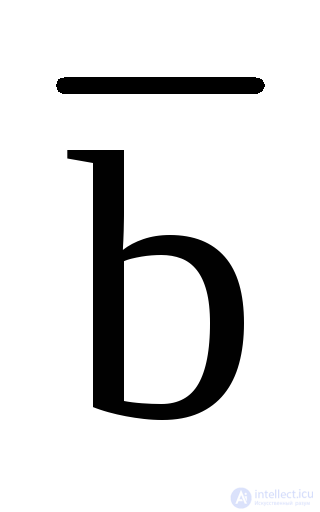
 d +
d + 
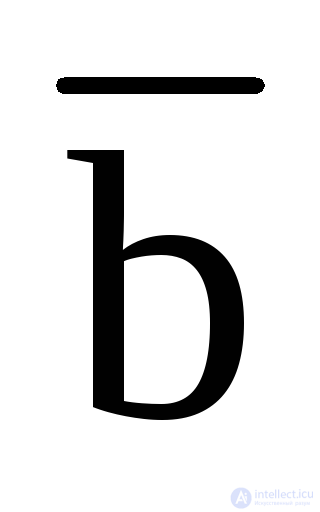 cd +
cd +  b
b  d + d
d + d 

 .
.
To write in the form of SKNF, you need to select from the table zero sets of variables, invert the variables in each of these sets, represent zero as constituents and make their conjunction.
SKNF: Y = (a + b +  + d) (a +
+ d) (a + 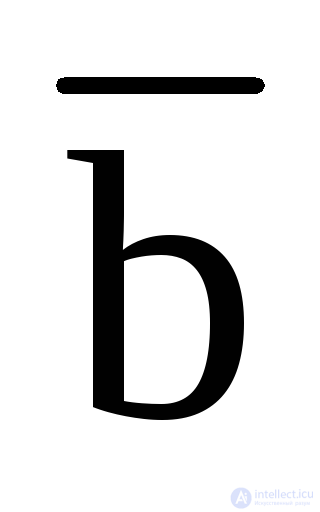 +
+  +
+  ) (
) (  + b + c +
+ b + c +  ) (
) (  +
+ 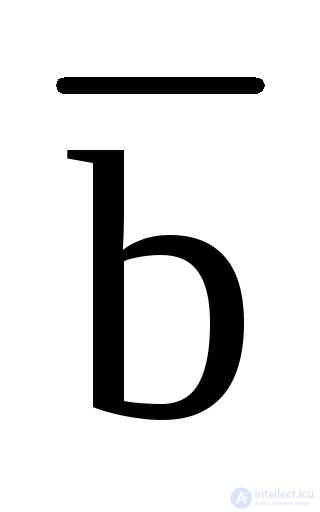 + c +
+ c +  ) (
) (  +
+  +
+  +
+  ).
).
Similarly, you can make SDNF and SKNF by decimal equivalents that define the Boolean function.
SDNF (perfect disjunctive normal form)
SKNF (perfect conjunctive normal form)
Each logical function has one SDNF and one SKNF.
The PDNF of a logical function is the disjunction of the constituent of the unit (minterm) corresponding to the sets of input variables for which the function is equal to 1.
In general, PDNF can be presented in the form:
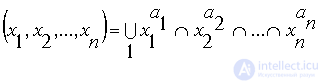
where is a 1 , and 2 , ..., and n is a binary set,

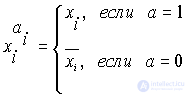
The FCNF of a logical function is the conjunction of the constituent of zero (maxster), corresponding to the input sets for which the function is equal to 0.
In general, SKNF can be presented in the form:
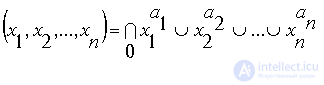
The constituent unit (zero) is an elementary conjunction (disjunction), which includes all n variables in direct or inverse form.
The form of representation of a logical function describing the operation of an element is chosen from considerations of minimizing the terms of the equation. PDNF is selected if the number of states of logical zero prevails in the truth table for a logical function, SKNF - a logical one
The algorithm of transition from the truth table of a logical function to its record in the form of SDNF :
The algorithm of transition from the truth table of a logical function to its record in the form of SKNF :
|
Perfect forms |
Formula |
|
Perfect conjunctive normal form (SKNF) - conjunction constituent zero |
|
|
Perfect disjunctive normal form (SDNF) - disjunction constituent units |
where is a 1 , and 2 , ..., and n is a binary set,
|
EXAMPLE:
| Table 2.1 | ||
| x1x2x3 | F1 | F2 |
| 000 | 0 | 0 |
| 001 | one | 0 |
| 010 | one | 0 |
| 011 | 0 | one |
| 100 | 0 | 0 |
| 101 | 0 | one |
| 110 | 0 | one |
| 111 | one | one |
F1 = / x1 / x2x3 v / x1x2 / x3 v x1x2x3
F2 = / x1x2x3 v x1 / x2x3 v x1x2 / x3 v x1x2x3
Another well-known form is called the perfect conjunctive normal form (SKNF) . It is built similarly to PDNF.
The constituent 0 is a function f (x1, x2, ... xn) taking the value 0 only on a single set.
The zero constituent is written as an elementary disjunction of all variables. Each set has its own constituent 0. For example, the set of 0110 variables x1x2x3x4 corresponds to the constituent of zero x1 v / x2 v / x3 v x4 . The SKNF is represented as a conjunction of a constituent of zero, corresponding to zero sets of a function. "
ПРИМЕР. Для рассмотренных функций в табл. 2.1 построим СКНФ:
F1=(x1 v x2 v x3) (x1 v /x2 v /x3) (/x1 v x2 v x3) (/x1 v x2 v /x3) (/x1 v /x2 v x3)
F2=(x1 v x2 v x3) (x1 v x2 v /x3) (x1 v /x2 v x3) (/x1 v x2 v x3)
Матрица Карно представляет собой специально организованные таблицы соответствия, обладающие тем замечательным свойством, что любые две соседние клетки матрицы определяют «соседние» наборы переменных, т.е. наборы, отличающиеся значением только одной переменной. Клетки, расположенные по краям матрицы, также являются соседними и обладают этим свойством. Это достигается благодаря кодированию столбцов и строк матрицы специальным циклическим кодом Грея.
Еще одним свойством матриц Карно является то, что при увеличении количества переменных на единицу матрица увеличивается вдвое, поскольку число клеток матрицы определяется показательной функцией «2n».
В клетках матрицы, как в таблице истинности, проставляются значения определяемой булевой функции – 0 или 1. Клетки, соответствующие фиктивным состояниям, обычно оставляют пустыми. For example, in fig. 2.1а представлена матрица Карно, определяющая функцию, заданную таблицей истинности (табл. 2.1). По сути дела, матрица Карно – это та же таблица состояний, но в более компактной форме.
In fig. 2.1b, c, d показаны соответственно матрицы Карно для двух, трех и пяти переменных.
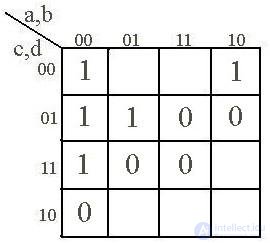
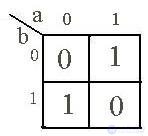
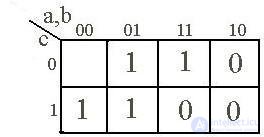
abc
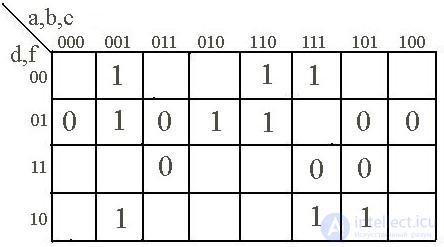
d
Fig. 2.1.
Comments
To leave a comment
Finite state machine theory
Terms: Finite state machine theory